数据结构

链表是一种线性存储结构，元素未存储的在连续的内存块中，而是通过类似指针的方式连接每一个节点。

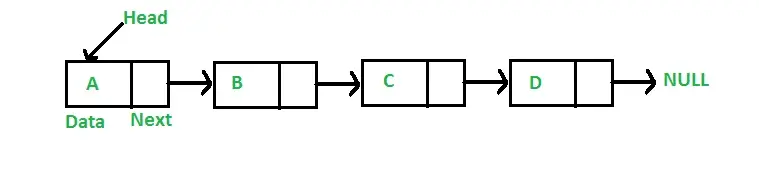
单链表

单链表是链表一种表现形式，是单向的，最后的节点执行 null ，除非出现环形链表。

单链表添加节点

单链表添加节点分为头部添加、中间添加以及尾部添加。

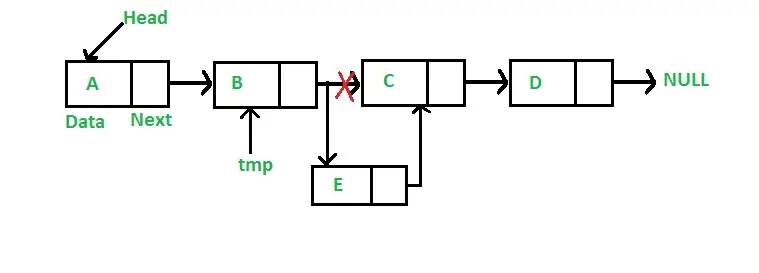
// 添加节点 头部以及尾部
LinkList.prototype.append = function (newElement) {
  var newNode = new Node(newElement);
  var curNode = this.head;
  while (curNode.next) {
    curNode = curNode.next;
  }
  curNode.next = newNode;
}

// 指定结点之后插入结点
LinkList.prototype.insert = function (newElement, element) {
  var curNode = this.findByValue(element);

  if (curNode == -1) {
    console.log('未找到结点');
    return;
  }
  var newNode = new Node(newElement);
  newNode.next = curNode.next;
  curNode.next = newNode;
}

单链表的实现

单链表的实现有实例化节点的构造函数以及整个单链表的构造函数

单链表的原型方式有：

• append 添加节点
• remove 删除指定节点
• findByValue 查找指定节点通过节点值
• findById 查找指定节点通过id
• findPrev 查找指定节点的上一个节点
• insert 插入节点在指定节点之后
• display 遍历节点

除了上述这些方法，还有其他的可以自定义的方法

// 链表
// 伪代码 结构
var linkList = {
  data: 'head',
  next: {
    data: 'first',
    next: {
      data: 'second',
      next: null
    }
  }
}

// 结点 - 内存块
function Node(element) {
  this.data = element;
  this.next = null;
}

function LinkList() {
  // 头结点
  this.head = new Node('head');

}

// 链表尾结点新增结点
LinkList.prototype.append = function (newElement) {
  var newNode = new Node(newElement);
  var curNode = this.head;
  while (curNode.next) {
    curNode = curNode.next;
  }
  curNode.next = newNode;
}


// 通过结点值查找结点
LinkList.prototype.findByValue = function (value) {
  // 遍历 从头结点

  var curNode = this.head.next;
  while (curNode != null && curNode.data != value) {
    curNode = curNode.next;
  }
  return curNode === null ? -1 : curNode;
}

// 通过index查找结点
LinkList.prototype.findByid = function (index) {
  var curNode = this.head.next;
  var pos = 0;
  while (curNode !== null && pos !== index) {
    curNode = curNode.next;
    pos++;
  }
  return curNode === null ? -1 : curNode;
}

// 查找指定结点的上一个结点
LinkList.prototype.findPrev = function (value) {
  var curNode = this.head;

  while (curNode.next !== null && curNode.next.data !== value) {
    curNode = curNode.next;
  }
  if (curNode.next === null) {
    return -1;
  }
  return curNode;
}

// 移除指定结点
LinkList.prototype.remove = function (value) {
  var prevNode = this.findPrev(value);
  if (prevNode == -1) {
    console.log('未找到结点');
    return
  }
  prevNode.next = prevNode.next.next;
}

// 遍历链表结构
LinkList.prototype.diaplay = function () {
  var curNode = this.head.next;
  while (curNode !== null) {
    console.log(curNode.data);
    curNode = curNode.next
  }
}


// 指定结点之后插入结点
LinkList.prototype.insert = function (newElement, element) {
  var curNode = this.findByValue(element);

  if (curNode == -1) {
    console.log('未找到结点');
    return;
  }
  var newNode = new Node(newElement);
  newNode.next = curNode.next;
  curNode.next = newNode;
}


var LLinkList = new LinkList();

console.log(LLinkList)

LLinkList.append('first');
LLinkList.append('second');
LLinkList.append('third');
LLinkList.append('five');


LLinkList.insert('four', 'third');
var findValue = LLinkList.findByValue('second');
console.log(findValue)

var findPrev = LLinkList.findPrev('four');
console.log(findPrev)

LLinkList.remove('first')

LLinkList.diaplay()

双链表

双链表相比单链表多了一个节点prev，指向其前一个节点

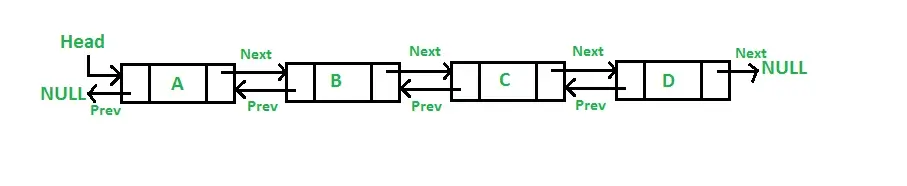
双链表实现

双链表的实现基础结构跟单链表差不多，节点构造函数多了prev属性。在初始化双链表的时候，增加了头尾节点，方便双链表的删除以及增加节点的操作。

下面主要实现了双链表的头尾添加节点以及删除节点

class LinkNode {
  constructor(val) {
    this.val = val;
    this.prev = null;
    this.next = null;
  }
}

class DoubleLinkList {
  constructor() {
    this.size = 0;
    this.head = new LinkNode('head')
    this.tail = new LinkNode('tail')
    this.head.next = this.tail;
    this.tail.prev = this.head;
  }
  // 头部插入节点
  addAtHead(node) {
    const curNode = this.head;
    const nodeNext = curNode.next;

    node.next = nodeNext;
    node.prev = curNode;

    curNode.next = node;
    nodeNext.prev = node;
    this.size++
  }
  // 尾部插入节点
  addAtTail(node) {
    const curNode = this.tail;
    const nodePrev = curNode.prev;

    node.next = nodePrev.next;
    node.prev = nodePrev;

    nodePrev.next = node;
    curNode.prev = node;
    this.size++
  }
  // 删除节点
  removeNode(node) {
    node.prev.next = node.next;
    node.next.prev = node.prev;
    this.size--;
  }
}

链表中双指针技巧

双指针技巧在链表的使用只能采用快慢指针的模式。这里收集了利用双指针解题的算法题。

• 环形链表
• 环形链表II
• 相交链表
• 删除链表的倒数第N个节点

环形链表

环形链表可以判断一个单链表是否有环，见下图

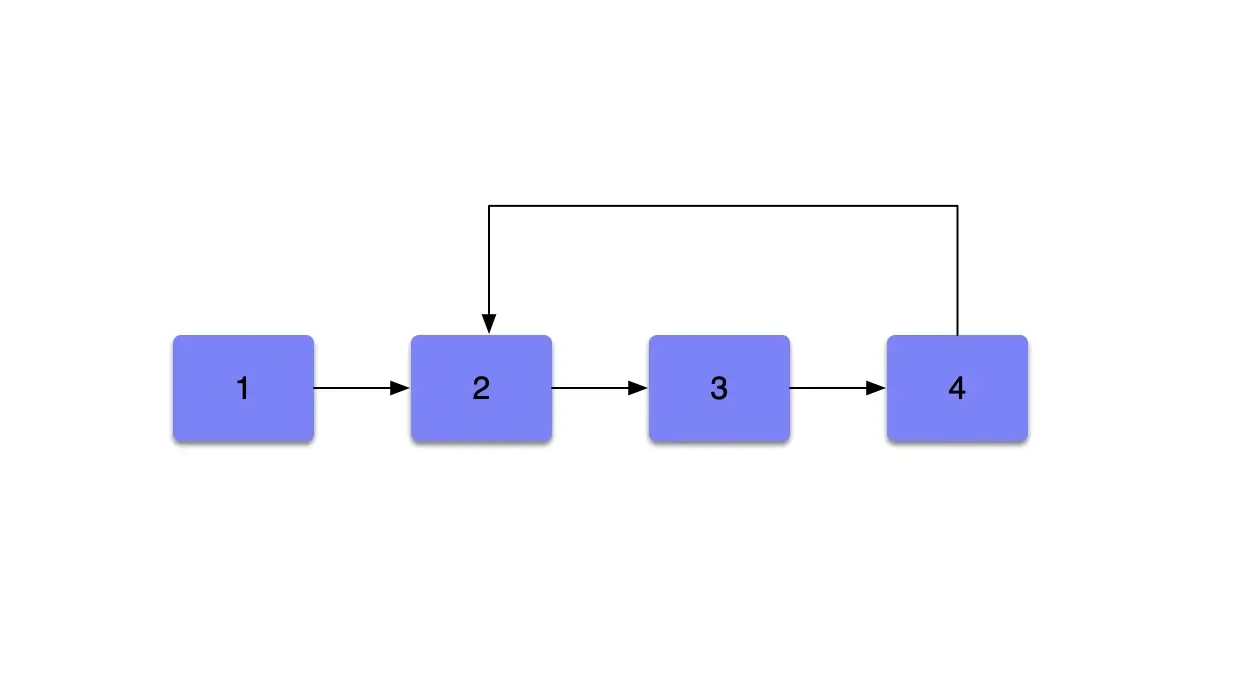
在考虑到空间复杂度，可以在当前内存中使用快慢指针技巧快速判断。

此方法可以称之为Floyd 判圈算法

const hasCycle = function(head) {
  if(head == null || head.next) return false;
  // 慢指针
  let slow = head;
  // 快指针
  let fast = head.next;
  // 快慢指针相遇 则说明有环
  while(slow != fast) {
    if(fast == null || fast.next == null) return false;

    slow = slow.next;
    fast = fast.next.next;
  }

  return true
}

环形链表II

环形链表II 在之前的基础上要**返回入环的第一个节点，也就是下面的节点2 **

在确认链表有环的前提下，新增一个指针，从链表头部开始移动，同时与快慢指针相遇的节点移动，最终两者都会相遇，相遇节点就是入环的第一个节点。

const detectCycle1 = (head) => {
  if(head == null || head.next == null) return null;
  let slow = head;
  let fast = head;
  // 判断是否有环
  while(fast !== null) {
    slow = slow.next;
    if(fast.next == null) return null;
    fast = fast.next.next;
    // 快慢节点向右 判断有环
    if(slow == fast) {
      let curNode = head;
      // 寻找入环的第一个节点
      while(slow != curNode) {
        slow = slow.next;
        curNode = curNode.next;
      }
      return slow;
    }
  }
  return null;
}

相交链表

如下图，两个单链表相交，返回相交的起始节点

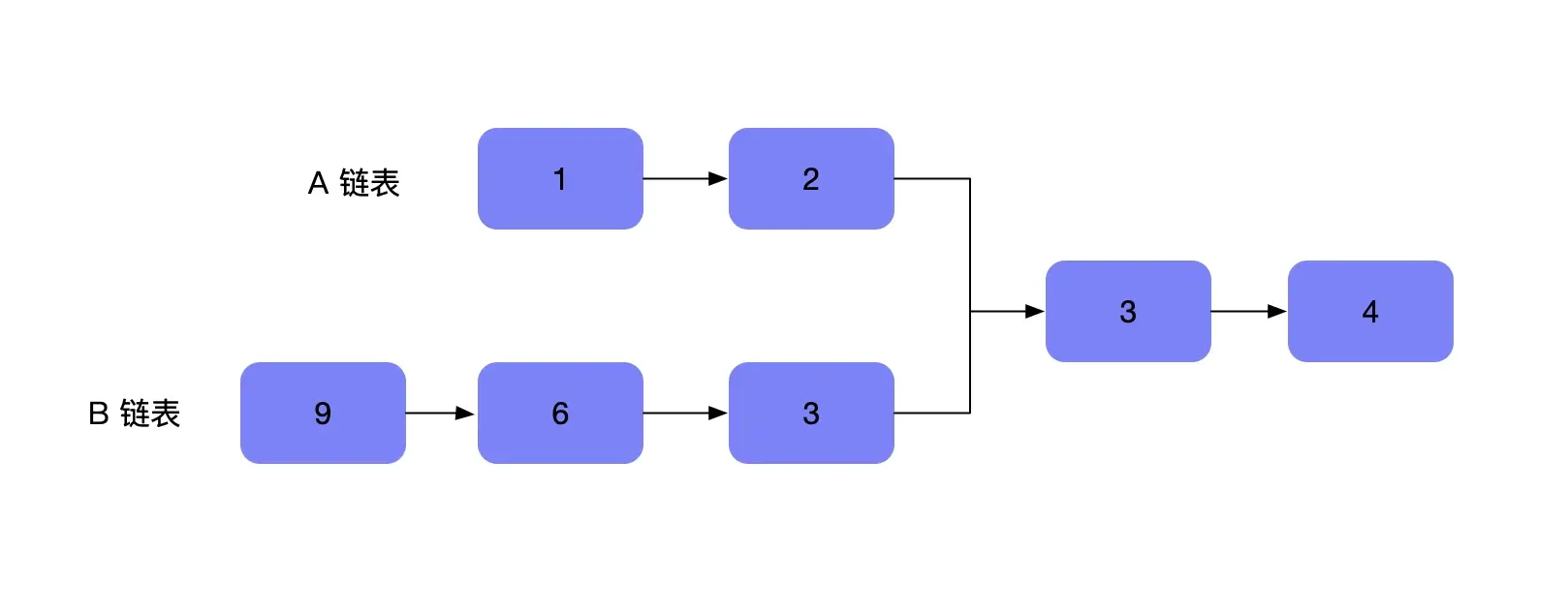
比较简单的方式可以用哈希表，不过这种方式额外增加了空间复杂度，最优的解法是在原地进行操作，也就是使用双指针模式。

A链表和B链表同时进行遍历，循环结束的条件是A链表和B链表当前的节点相同。

const getIntersectionNode = (headA, headB) => {
  if(headA == null || headB == null) return null;

  let nodeA = headA;
  let nodeB = headB;

  while(nodeA != nodeB) {
     nodeA = nodeA !== null ? nodeA.next : headB;
     nodeB = nodeB !== null ? nodeB.next : headA;
  }

  return nodeA
}

上面循环体中当链表A到达尾部的时候，将链表B头结点指向nodeA，同理链表B到达尾结点时，将链表A头结点指向B，这样下次循环的时候两个链表一定会相遇。

删除链表的倒数第N个节点

如下图，需要删除4这个节点

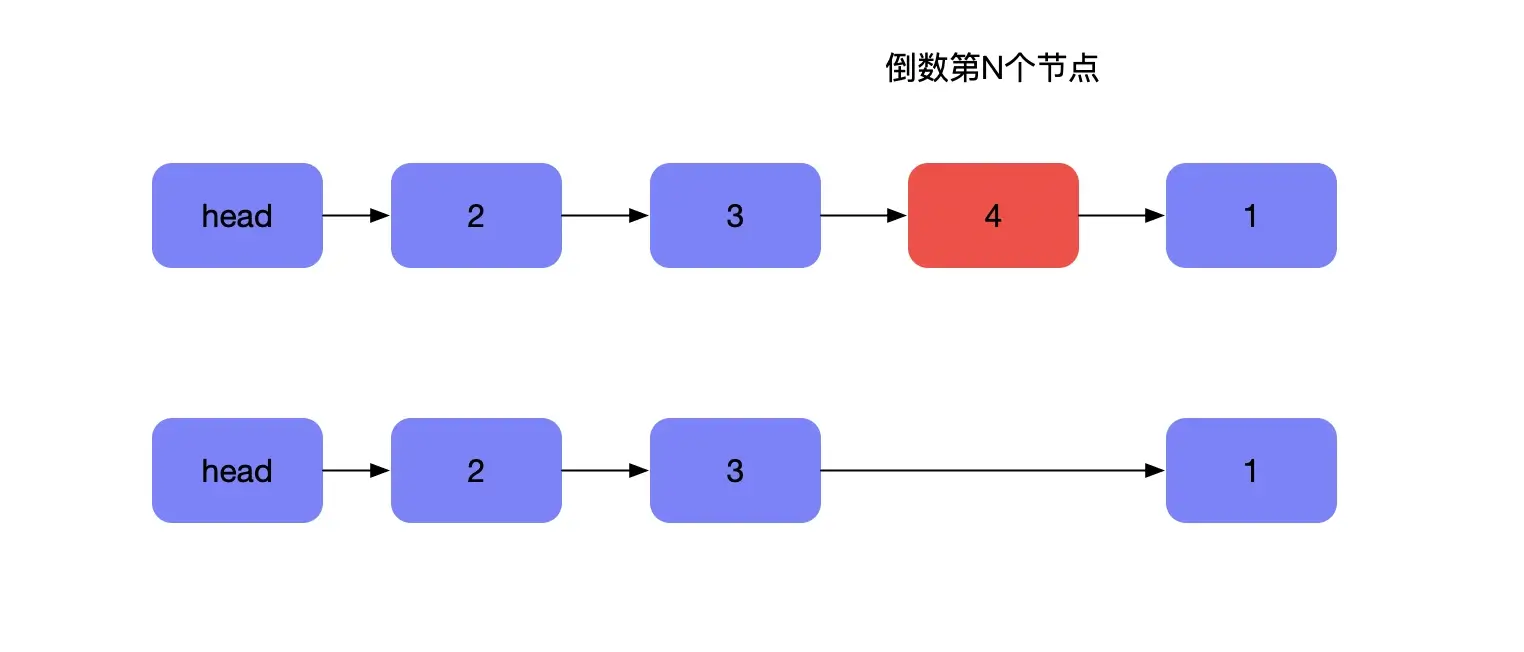
一种简单的思路是计算链表的长度，得到需要删除节点的顺序位置，然后再遍历链表，删除节点

const removeNthFromEnd = function(head, n) {
  if(head == null || head.next == null) return head.next;

  let size = 0;
  let index = 0;
  let fast = head;
  let slow = head;

  while(curNode !== null) {
    size++;
    curNode = curNode.next;
  }

  while(slow.next !== null) {
    if(index == size - n - 1) {
      slow.next = slow.next.next;
      return head;
    }
    index++;
    slow = slow.next
  }
  return head.next
}

这种方式是比较简单易理解的，时间和空间复杂度上分别为O(L) O(1) 。

另一种方式就是**双指针模式，**定义快慢指针，以及哨兵节点（方便处理链表）

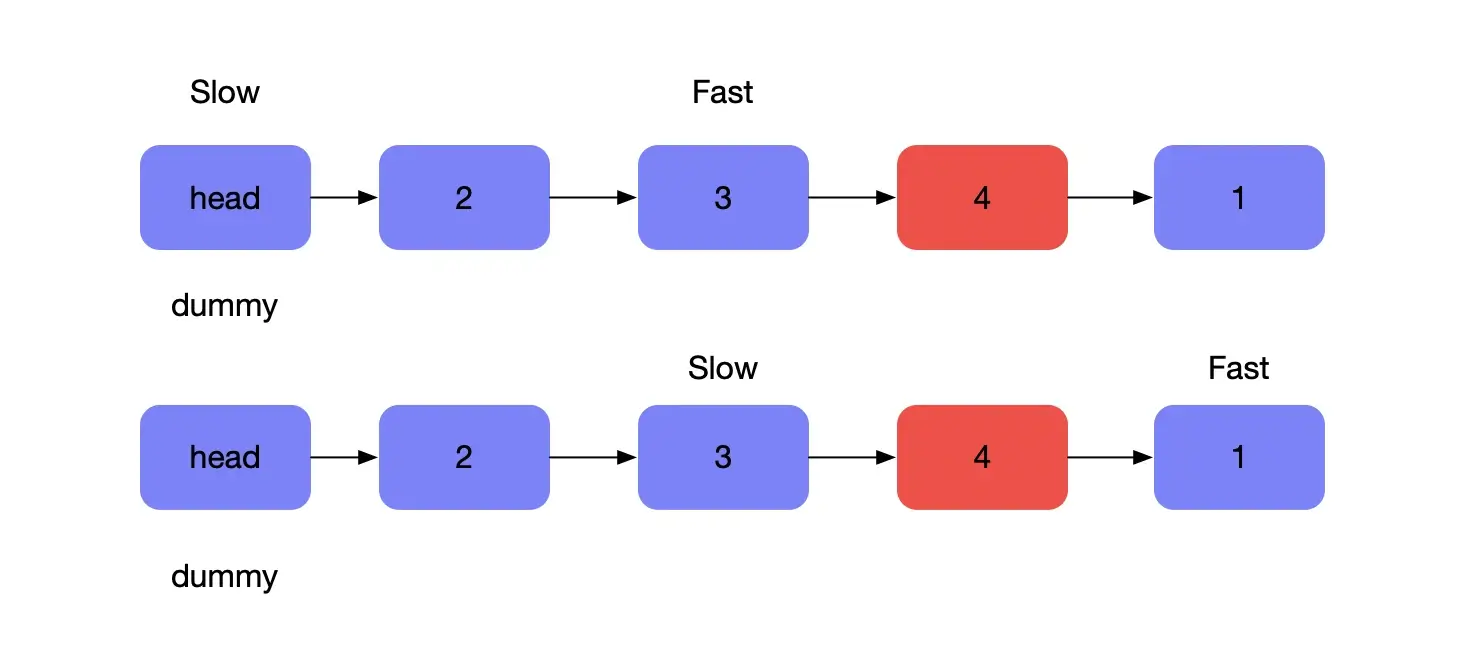
先让快指针移动 n个步骤，这样之后快慢指针同时移动，直到快指针指向null ，此时慢指针指向的就是待删除的节点。如下图，为了方便删除节点，给链表头部新增了dummy 节点。

const removeNthFromEnd1 = function(head, n) {

  let dummny = new LinkNode('head', head); // dummy.next = head

  let fast = head;
  let slow = dummny;

  for(let i = 0; i < n; i++) {
    fast = fast.next;
  }

  while(fast !== null) {
    fast = fast.next;
    slow = slow.next;
  }
  slow.next = slow.next.next;
  return dummuy.next;
}

链表经典问题

• 反转链表
• 移除链表元素
• 奇偶链表
• 回文链表
• 对链表进行插入排序
• 链表排序
• 合并两个有序链表
• 复制带随机指针的链表
• 两数相加
• 旋转链表
• LRU 缓存机制
• 合并K个升序链表

反转链表

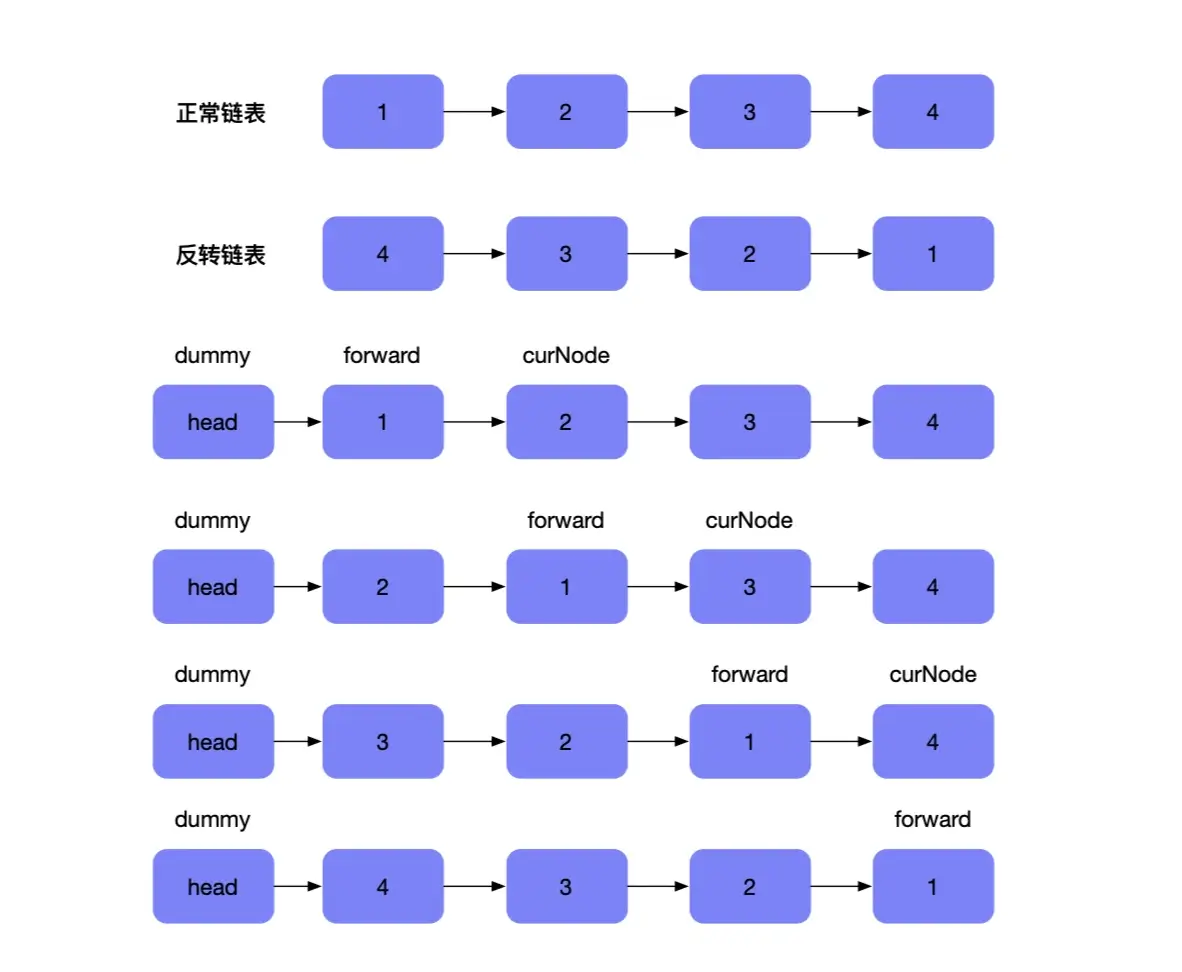
如上图流程所示

在链表的基础上新增了一个头结点 head , 定义了两个指针 forward(慢指针) 和 curNode(快指针) ，将快指针对应的节点移动到 head 节点之后，最后移动快指针，以此类推，所有的节点都移动到了头结点之后。

const reverseList = function(head) {
  let dummy = new LinkNode('head')
  dummy.next = head;

  let forwardNode = dummy.next;
  let curNode = forwardNode.next;

  while(curNode != null) {
    forwardNode.next = curNode.next;
    curNode.next = dummy.next;
    dummy.next = curNode;

    curNode = forwardNode.next;
  }
  return dummy.next
}

移除链表元素

如下图，删除链表中给定值的节点 4

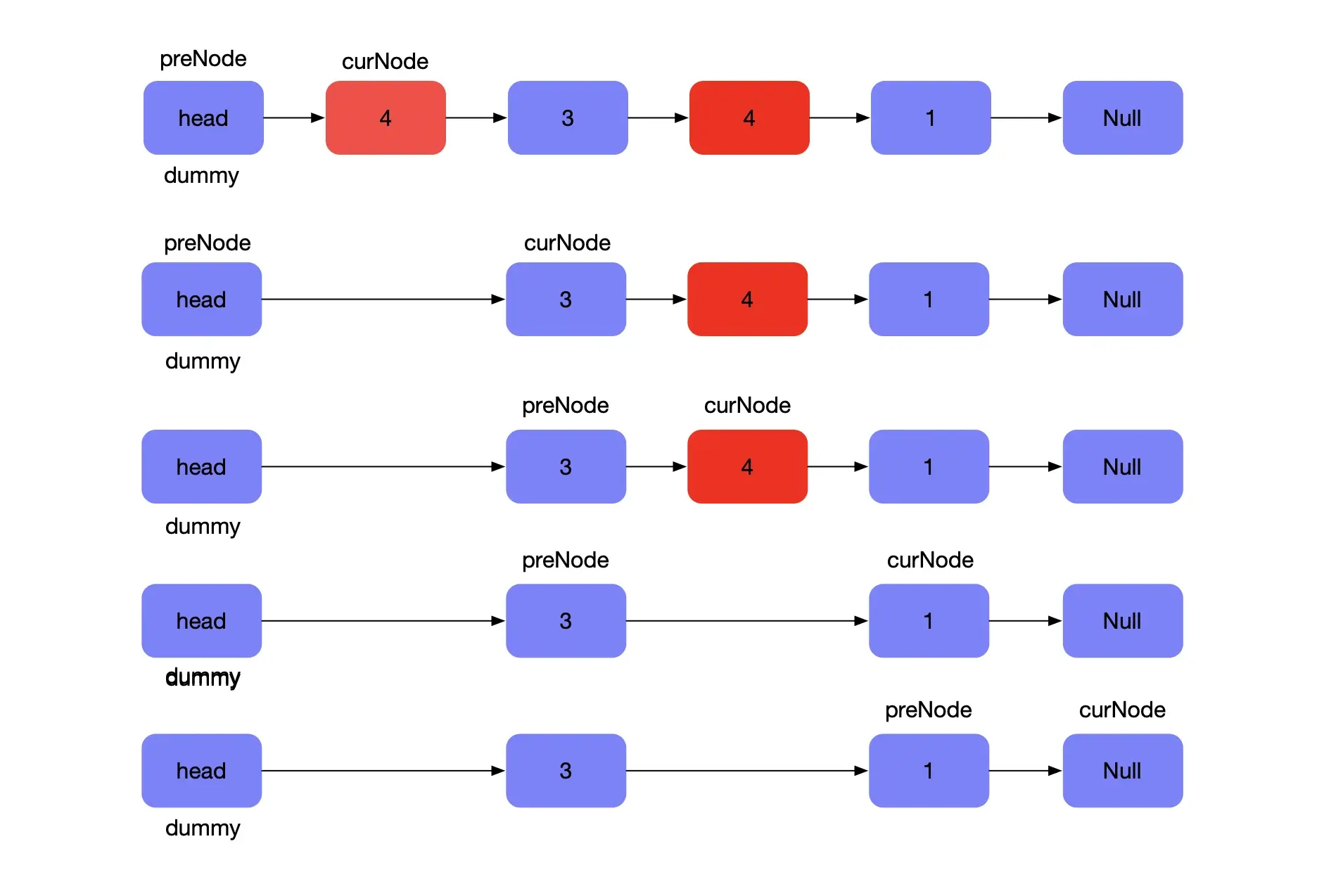
可以看到，dummy 节点是自定义的头节点，这里定义了一个哨兵节点（为了删除节点）preNode 。然后遍历链表，如果有需要删除的节点，哨兵节点指向了删除节点的 next ，反之，哨兵节点跟着当前节点curNode移动，直到链表遍历结束。

const removeElements = function(head, val) {

  let dummy = new LinkNode('head')
  dummy.next = head;

  let prevNode = dummy;
  let curNode = head;

  while(curNode) {
    if(curNode.val == val) {
      prevNode.next = curNode.next;
    }else {
      prevNode = curNode
    }
    curNode = curNode.next;
  }

  return dummy.next
};

奇偶链表

给定一个单链表，把所有的奇数节点和偶数节点分别排在一起。请注意，这里的奇数节点和偶数节点指的是节点编号的奇偶性，而不是节点的值的奇偶性。 -- from LeetCode

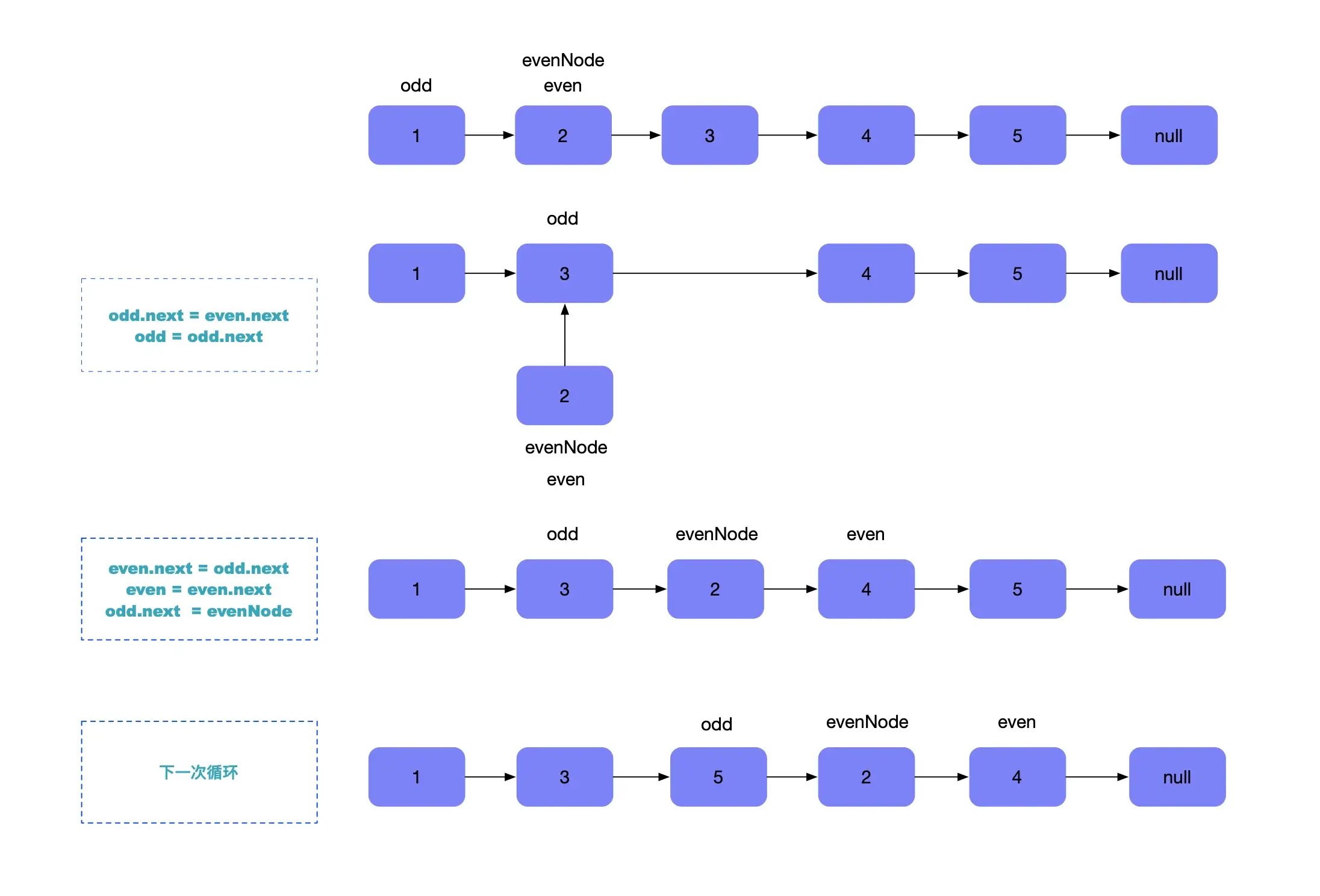
上图所示，根据题意，链表的第一个节点肯定是奇节点，下一个是偶节点，以此类推。定义两个移动指针odd （奇节点） 和 even （偶节点），初次之外，定义一个偶节点 evenNode，指向偶节点链头，目的是将奇链表的尾节点指向该偶链表的头部。

const oddEvenList = function(head) {
  if(head == null) return head;

  let odd = head;
  let even = head.next;
  // 偶链表头部
  let evenNode = even;

  while(even !== null && even.next !== null) {
    odd.next = even.next;
    odd = odd.next;
    even.next = odd.next;
    even = even.next;
    // 当前循环奇链表尾部指向偶链表头部
    odd.next = evenNode;
  }
  return head;
}

回文链表

回文链表跟回文的概念是类似的，但是判断回文链表不能使用双向指针，因为链表只能使用快慢指针。

如下图，使用快慢指针来解决回文链表的图解

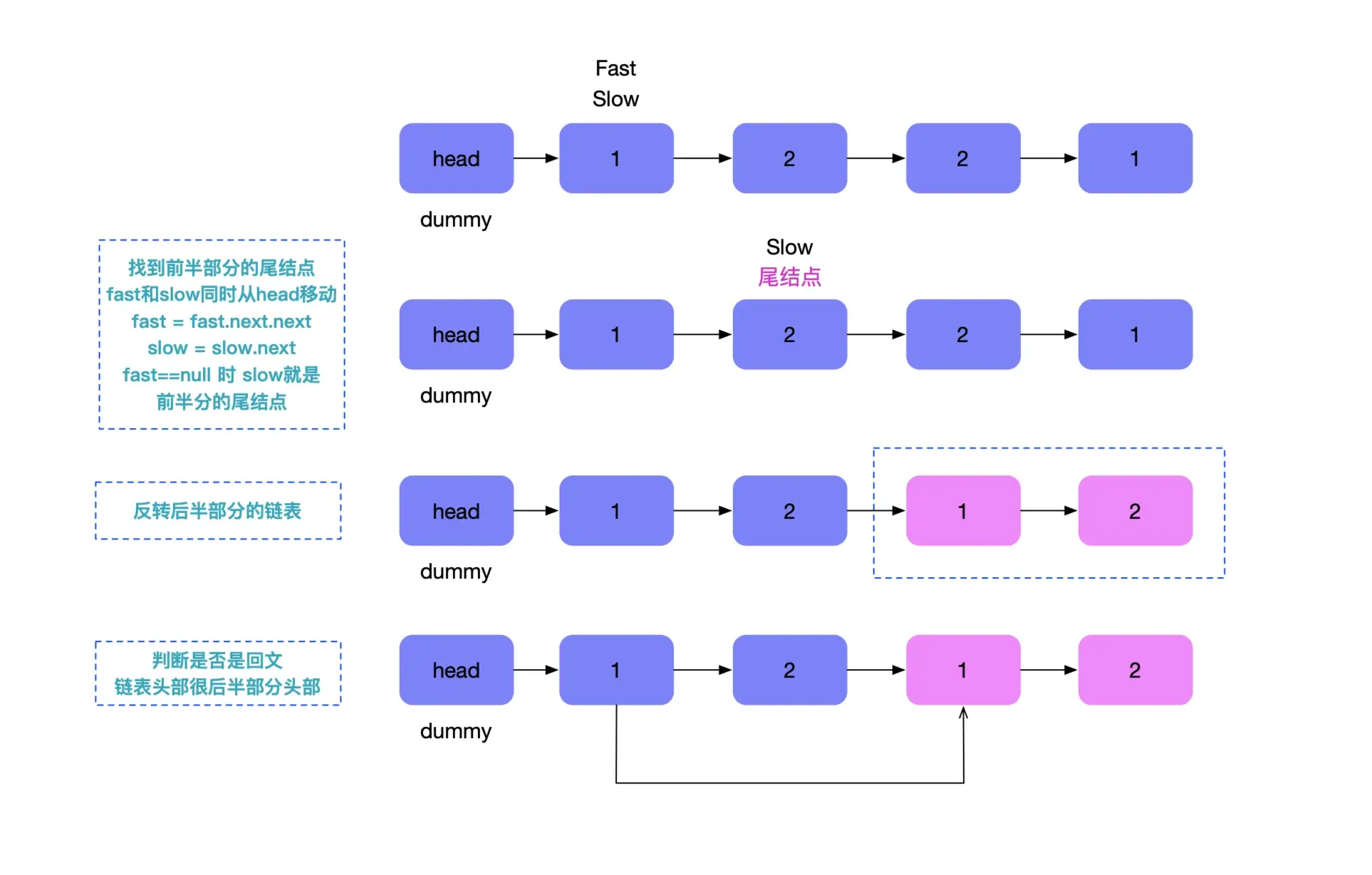
首先，将链表分为两部分，将后半部分进行反转，然后将前半部分跟后半部分进行对比，得出是否是回文链表

// 链表分成两部分 返回前半部分的尾结点
const firstHalfLink = (head) => {
  let fast = head;
  let slow = head;

  while(fast.next !== null && fast.next.next != null) {
    slow = slow.next;
    fast = fast.next.next;
  }
  return slow;
}

// 反转链表
const reverseLink = (head) => {
  let dummy = new LinkNode('head');
  dummy.next = head;

  let forwardNode = dummy.next;
  let curNode = forwardNode.next;

  while(curNode !== null) {
    forwardNode.next = curNode.next;
    curNode.next = dummy.next;
    dummy.next = curNode;

    curNode = forwardNode.next
  }
  return dummy.next
}

// 是否是回文链表
const isPalindrome = (head) => {
  if(head == null) return true;

  const firstListNode = firstHalfLink(head);
  const secondListNode = reverseLink(firstListNode.next);

  let result = true;
  let f = head;
  let s = secondListNode;

  while(result && s.next != null) {
    if(f.val !== s.val) return false;
    f = f.next;
    s = s.next;
  }

  return result
}

链表进行插入排序

关于插入排序，可以到 排序算法

下图展示了链表插入排序的图示

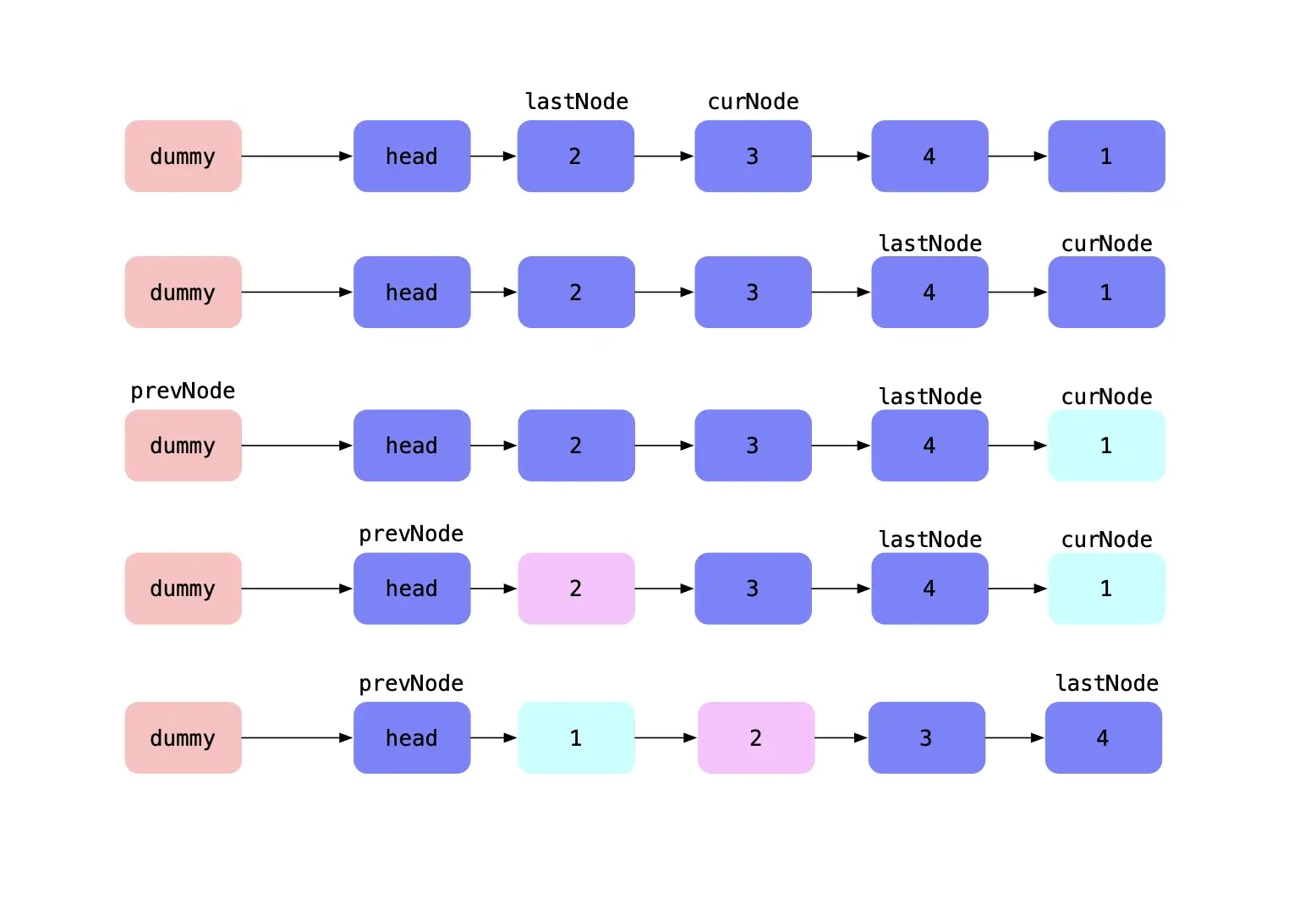
首先，需要一个哨兵节点来记录整个链表的变化。

其次，需要两个节点来对比大小，lastNode 和 curNode

如果lastNode 大于 curNode ，继续移动curNode和lastNode

否则从链表头部，如果遇到大于curNode的节点，将curNode和当前节点交换

const insertionSortList = (head) => {
  if(head == null) return head;
  let dummy = new ListNode('head');
  dummy.next = head;

  let lastNode = head;
  let curNode = head.next;
  while(curNode != null) {
    if(lastNode.val <= curNode.val) {
      lastNode = lastNode.next;
    }else {
      let prevNode = dummy;
      while(prevNode.next.val <= curNode.val) {
        prevNode = prevNode.next;
      }
      lastNode.next = curNode.next;
      curNode.next = prevNode.next;
      prevNode.next = curNode
    }
    curNode = lastNode.next
  }
  return dummy.next;
}

链表排序（归并）

合并两个有序链表

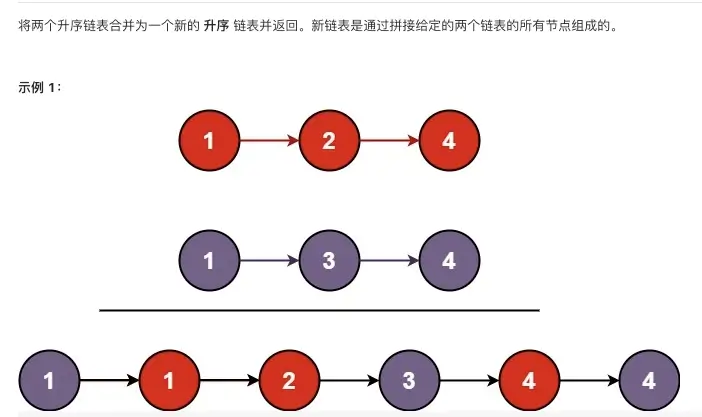
合并 + 排序

最容易想到的解法，就是先合并成一个链表，然后进行排序

var mergeTwoLists1 = function(l1, l2) {

  if(l1 == null && l2 == null) return null;

  if(l1 == null) return l2;

  if(l2 == null) return l1;

  let cur = l1

  while(cur !== null) {
    if(cur.next == null) {
      cur.next = l2;
      break;
    }
    cur = cur.next
  }

  let dummy = new ListNode('head', l1)
  let lastNode = l1;
  let curNode = l1.next;

  while(curNode != null) {
    if(lastNode.val <= curNode.val) {
      lastNode = lastNode.next;
    }else {
      let pre = dummy;
      while(pre.next.val <= curNode.val) {
        pre = pre.next;
      }
      lastNode.next = curNode.next;
      curNode.next = pre.next;
      pre.next = curNode
    }
    curNode = lastNode.next;
  }

  return dummy.next;

};

递归方式

const mergerTwoList = (head1, head2) => {
  if(head1 == null) return head2;

  if(head2 == null) return head1;

  if(head1.val <= head2.val) {
    head1.next = mergerTwoList(head1.next, head2)
    return head1
  }else {
    head2.next = mergerTwoList(head1, head2.next)
    return head2
  }
}

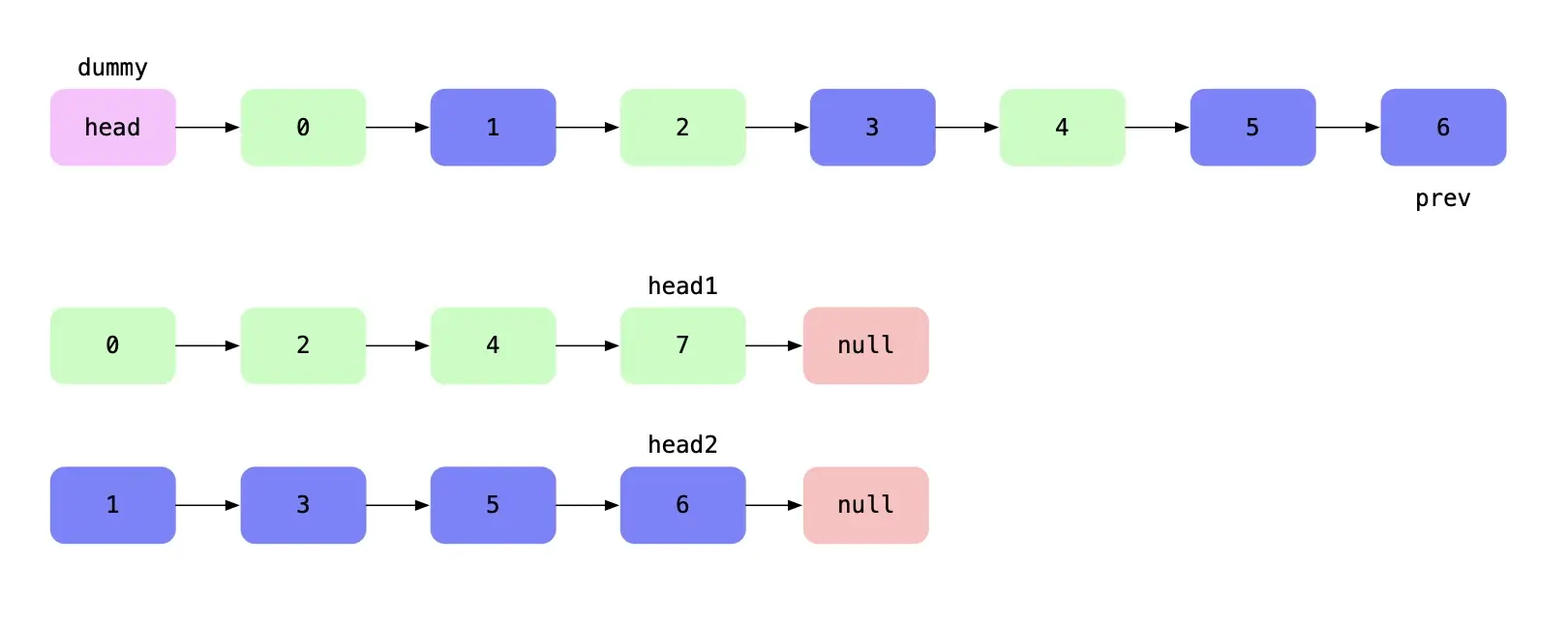
递归方式改为遍历

const mergerTwoList = (head1, head2) => {

  const dummy = new LinkNode('head')
  let prevNode = dummy

  while(head1 != null && head2 != null) {
    if(head1.val <= head2.val) {
      prevNode.next = head1;
      head1 = head1.next
    }else {
      prevNode.next = head2;
      head2 = head2.next;
    }
    prevNode = prevNode.next;
  }
  prevNode.next = head1 == null ? head2 : head1;
  return dummy.next
}

复制带随机数的链表

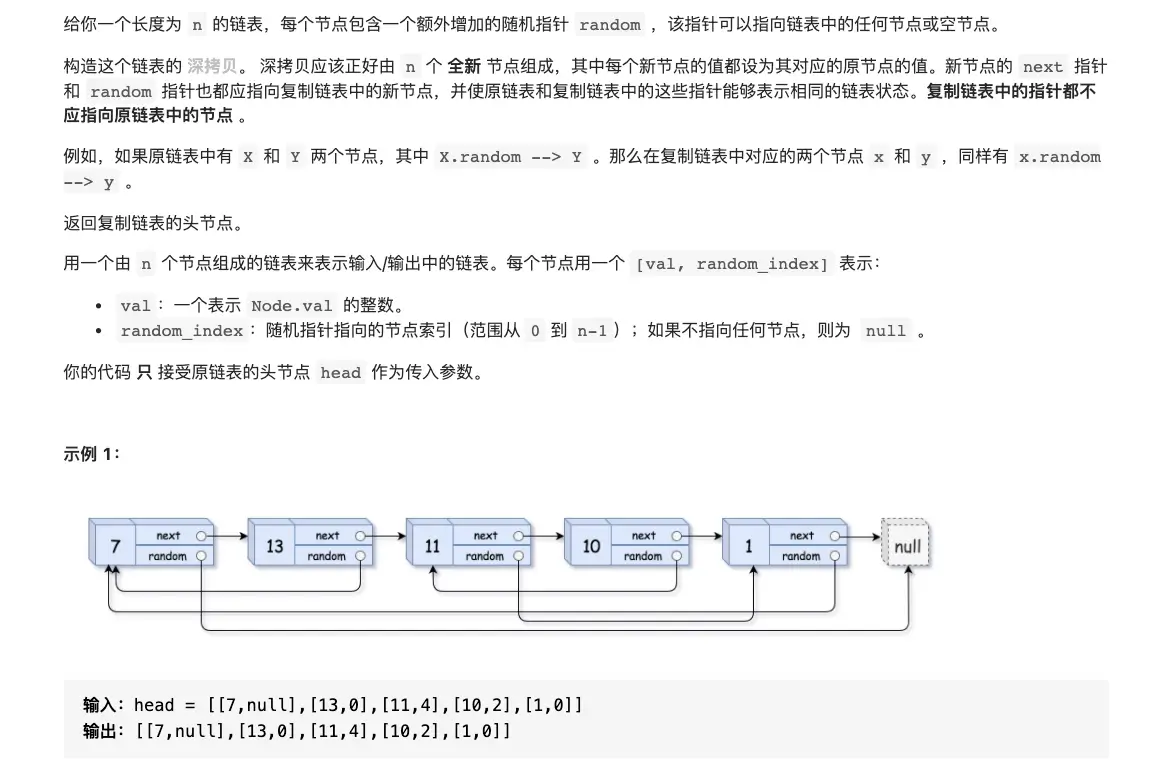
function Node(val, next, random) {
  this.val = val;
  this.next = next;
  this.random = random;
}

const copyListRandom = (head) => {

  if(head == null) return null;

  // 复制每一个节点
  for(let node = head; node != null; node = node.next.next) {
    node.next = new Node(node.val, node.next, null)
  }
  // 复制没一个节点的random
  for(let node = head; node != null; node = node.next.next) {
    const newNode = node.next;
    newNode.random = node.random != null ? node.random.next : null
  }

  // 还原原来节点
  // 组合新的复制节点
  const headNode = head.next;
  for(let node = head; node != null; node = node.next) {
    const newNode = node.next;
    node.next = node.next.next;
    newNode.next = newNode.next != null ? newNode.next.next : null
  }
  return headNode
}

两数相加

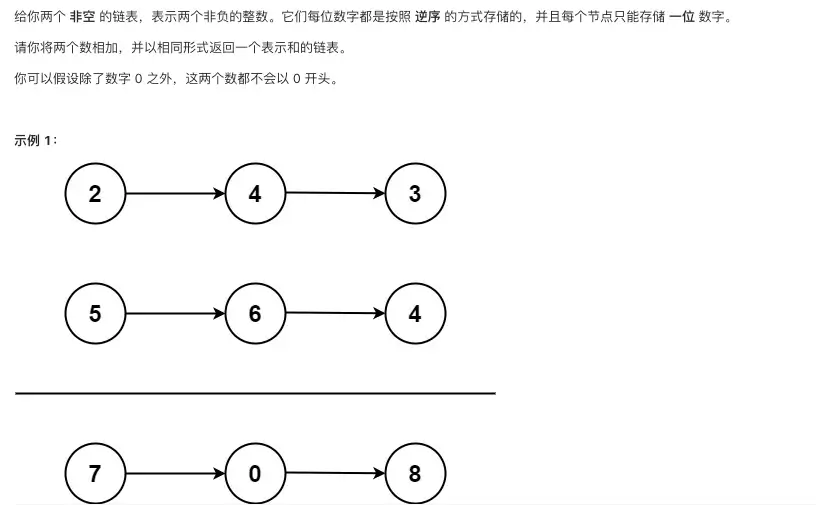
可以想到的方式是同时遍历两个链表，然后根据是否有进位，如果有进位，则跟下两位节点进行计算，直到链表遍历结束，如果还有进位，则添加进链表中。

const addTwoNumbers = (l1, l2) => {

   let head1 = l1;
   let head2 = l2;

   let dummy = new ListNode(0);
   let prev = dummy;

   let nextNum = 0;

   while(head1 != null || head2 != null) {
     const head1Val = head1 == null ? 0 : head1.val;
     const head2Val = head2 == null ? 0 : head2.val;

     const num = head1Val + head2Val;

     const digist = (num + nextNum) % 10;
     nextNum = ~~((num + nextNum) / 10);

     prev.next = new ListNode(digist);

     head1 = head1 && head1.next;
     head2 = head2 && head2.next;
     prev = prev.next
   }
   if(nextNum > 0) {
     prev.next = new ListNode(nextNum);
   }
   return dummy.next
}

旋转链表

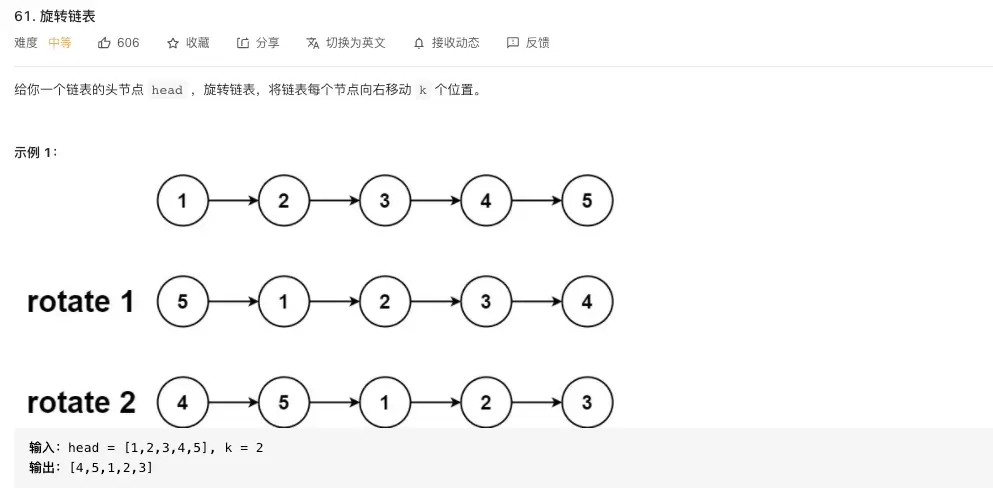
看题意，如果不用构造环来解决的话，最能想到的就是是暴力法，找到尾结点，然后将其插入到头结点上。这里将头结点加入到哨兵节点之后，方便头节点的操作。

使用双指针，快指针找到尾结点，慢指针指向头结点，然后插入到头结点，之后快慢指针重新指向头结点，依次循环，直到操作 k 次。

const rotateRight_bad = (head, k) => {
  if(head == null || head.next == null || k == 0) return null;

  let dummy = new ListNode(0, head);
  let num = 0;

  let prev = dummy.next;
  let node = prev.next;

  while(num <= k) {

    while(node.next != null) {
      node = node.next;
      prev = prev.next;
    }
    prev.next = node.next;

    node.next = dummy.next;
    dummy.next = node

    prev = dummy.next;
    node = prev.next;
    num++
  }
  return dummy.next
}

为什么说这种解法是暴力呢？因为时间复杂度太高了 O(n * k) n 为链表的长度。

构造环解法

这种解法是将链表组成一个环形链表，根据要旋转的次数，然后再将链表断开。

这里的重点是旋转的次数，如果 k >= n , 那么就是旋转了一周之后，在旋转 k % n 次即可。因此可得，链表旋转 n - k % n 次可得到最后的新链表

const rotateRight_right = (head) => {
  if(head == null || head.next == null || k == 0) return head;

  let len = 1;

  let node = head;

  while(node.next != null) {
    node = node.next;
    len++
  }
  // k >= n
  let step = len - (k % len)
  node.next = head;

  while(step) {
    node = node.next;
    step--;
  }

  const newHead = node.next;
  node.next = null;

  return newHead;
}

LRU缓存机制

此题也是经典面试题，除了题意，要求get 和 put操作的时间复杂度都是O(1) ，这样的数据结构可以联想到链表，因为在添加数据的时候可能存在删除数据，要保证put操作的时间复杂度为 O(1)，插入操作和删除操作都要保持O(1)的时间复杂度，这样一来，可以暂时定为双链表，不过前提条件是先查找到该节点，这个可以用哈希表。

综述得到，get 和 put 操作的时间复杂度都为O(1)

class LinkNode {
  constructor(key, val) {
        this.key = key;
        this.val = val;
        this.prev = null;
        this.next = null
    }
}

class DoubleLinkList {
    constructor() {
        this.size = 0
        this.head = new LinkNode('head');
        this.tail = new LinkNode('tail');
        this.head.next = this.tail;
        this.tail.prev = this.head
    }
    addAtHead(newNode) {
        // const newNode = new LinkNode(val)
        const head = this.head;
        newNode.next = head.next;
        newNode.prev = head;
        head.next.prev = newNode;
        head.next = newNode;
        this.size++;
    }

    addAtTail(newNode) {
        // const newNode = new LinkNode(val)
        const tail = this.tail;
        const last = tail.prev;

        newNode.next = tail;
        newNode.prev = last;

        last.next = newNode;
        tail.prev = newNode;

        this.size++
    }

    moveToHead(node) {
        this.removeNode(node)
        this.addAtHead(node)
    }

    removeNode(node) {
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }

    removeTail() {
        const node = this.tail.prev
        this.removeNode(node)
        return node
    }
}

/**
 * @param {number} capacity
 */
var LRUCache = function(capacity) {
    this.capacity = capacity;
    this.size = 0;
    this.cache = new Map();
    this.dLink = new DoubleLinkList()
};

/**
 * @param {number} key
 * @return {number}
 */
LRUCache.prototype.get = function(key) {
    const node = this.cache.get(key)
    if(!node) {
        return -1;
    }else {
        this.dLink.moveToHead(node)
        return node.val
    }
};

/**
 * @param {number} key
 * @param {number} value
 * @return {void}
 */
LRUCache.prototype.put = function(key, value) {
    const node = this.cache.get(key)
    if(node == null) {
        const newNode = new LinkNode(key, value);
        this.size++;
        this.cache.set(key, newNode)
        this.dLink.addAtHead(newNode)
        if(this.size > this.capacity) {
            const tailNode = this.dLink.removeTail()
            this.cache.delete(tailNode.key)
            this.size--;
        }
    }else {
        node.val = value
        this.dLink.moveToHead(node)
    }
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * var obj = new LRUCache(capacity)
 * var param_1 = obj.get(key)
 * obj.put(key,value)
 */