无法捉摸的排序算法

排序算法是日常开发中常用的一种算法。排序算法有很多种，冒泡、选择、插入、快速、归并以及希尔排序等。每种排序算法都有一定的优缺点。首先从最简单的冒泡排序开始。

时间复杂度为O(n^2)

冒泡排序

下图为动图演示

排序冒泡会有两层循环，分为外循环和内循环。外循环负责整个数组的循环，内循环的区间随着外循环的区间变化而变化，内循环判断相邻元素大小，从而进行元素互换。

// 元素交换
function swap(arr, a, b) {
  let tmp = arr[a];
  arr[a] = arr[b];
  arr[b] = tmp;
}

// 位运算 进行元素交换
function swap(arr, a, b) {
  arr[a] = arr[a] ^ arr[b]
  arr[b] = arr[b] ^ arr[a]
  arr[a] = arr[a] ^ arr[b]
}

内循环判断相邻元素之间的大小 ，从而进行位置互换

// 冒泡算法 解法一
function bubbleSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length - 1; j++) {
      if(arr[j] > arr[j + 1])  {
        swap(arr, j, j+1)
      }
    }
  }
}

从动态图中不难发现，外循环每循环一次，数组后面的元素的顺序已经排好了，因此这是一部分没有必要的循环，可以在解法一的基础上优化，减少循环的次数， j = arr.length - 1 - i

// 冒泡算法 解法二 优化时间复杂度
function bubbleSort(arr) {
  console.time('bubble start')
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length - 1 - i; j++) {
      if(arr[j] > arr[j + 1])  {
        swap(arr, j, j+1)
      }
    }
  }
  console.timeEnd('bubble start')
}

可以看到，解法二在内循环的区间随着外循环的区间变化，这样内循环的判断就是在未排序好的区间进行循环，这样最大限度的节省了时间复杂度。

除此之外，当内层排序结束之后，外层循环可能还没有结束，因此多出了一些不必要的循环，可以使用一个标识来判断。

// 冒泡排序 解法三 优化内层循环结束外层还在遍历的问题
function bubbleSort(arr) {
  let swaped = true;
  for(let i = 0; i < arr.length; i++) {
    if(!swaped) break;
    // 每一次排序都要重置swaped
    swaped = false;
    for(let j = 0; j < arr.length - 1 - i; j++) {
      if(arr[j] > arr[j+1]) {
        swap(arr,j,j+1)
        swaped = true
      }
    }
  }
}

除上述解决已经排好序了外层还在运行的问题。还有一种场景，一个数组中除了无序部分还有一部分是排序好的。

如果这种使用上述解法，那会有很多的无用的操作。最好的方式是找到有序部分和无序部分的边界，然后只在无序部分进行排序，这样就减少了无用的操作。

function bubbleSort(arr) {
  // 最后一次交换的位置
  let lastExchangeIndex = 0;
  // 无序边界
  let sortBorder = arr.length - 1;

  for(let i = 0; i < arr.length - 1; i++) {
    let swaped = true;
    for(let j = 0; j < sortBorder; j++) {

      if(arr[j] > arr[j+1]) {
        swap(arr, j, j+1)
        swaped = false;
        lastExchangeIndex = j
      }
    }
    // 将以排序好的位置给到无序边界
    sortBorder = lastExchangeIndex;
    if(swaped) break;
  }
}

选择排序

下图为动图展示

可以看到，选择排序也是两重循环，外循环的第一个元素和内循环剩下的元素进行比较，将最小的元素放到第一个位置上，以此类推。

// 选择排序
function selectSort(arr) {
  console.time('select start')
  let min
  for (let i = 0; i < arr.length - 1; i++) {
    min = i;
    for (let j = i + 1; j < arr.length; j++) {
      if(arr[min] > arr[j]) {
        min = j
      }
    }
    if(min != i) swap(arr, i, min);
  }
  console.timeEnd('select start')
}

插入排序

下图为动图展示

插入排序也有两层循环，外层循环遍历每一个元素，内层循环对外层循环选中的选中的元素跟前一个元素 进行比较，如果选中的元素小于前一个元素，则将前一个元素后移，以此类推。

// 插入排序
function insertSort(arr) {
  console.time('insert start')
  let tmp, inner;
  for (let outer = 1; outer < arr.length; outer++) {
    const tmp = arr[outer];
    let inner = outer
    while (inner > 0 && arr[inner - 1] > tmp) {
      arr[inner] = arr[inner - 1]
      inner--
    }
    arr[inner] = tmp
  }
  console.timeEnd('insert start')
}

三种基本排序对比

这三种基本排序算法基本已经写完了，但是哪个是最优的呢，下面通过耗时来进行比较

// 生成随机数组
function randomArr(num) {
  let arr = []
  for (let i = 0; i < num; i++) {
    arr[i] = Math.floor(Math.random() * (num+1))
  }
  return arr
}
// 生成100个随机数
let testArr = randomArr(100);
bubbleSort(testArr); // bubble start: 0.76513671875 ms
selectSort(testArr); // select start: 0.239990234375 ms
insertSort(testArr); // insert start: 0.02197265625 ms

// 生成1000个随机数
let testArr = randomArr(1000);
bubbleSort(testArr); // bubble start: 4.07421875 ms
selectSort(testArr); // select start: 3.81494140625 ms
insertSort(testArr); // insert start: 4.828125 ms

// 生成10000个随机数
let testArr = randomArr(10000);
bubbleSort(testArr); // bubble start: 162.80908203125 ms
selectSort(testArr); // select start: 83.802001953125 ms
insertSort(testArr); // insert start: 0.68994140625 ms

可以看到，随着测试数量的增加，插入排序的耗时越来越少，在测试数量较少时，三种算法的耗时差不多。不过判断哪种算法最优，还要进行大量的数据进行测试。

时间复杂度为O(nlogn)

希尔排序

快速排序

快速排序是处理大量数据最快的一种算法，其核心思想是分而治之，采用递归的方式将数组分为多个单元，每个单元进行排序，最终依次将每个单元合并。

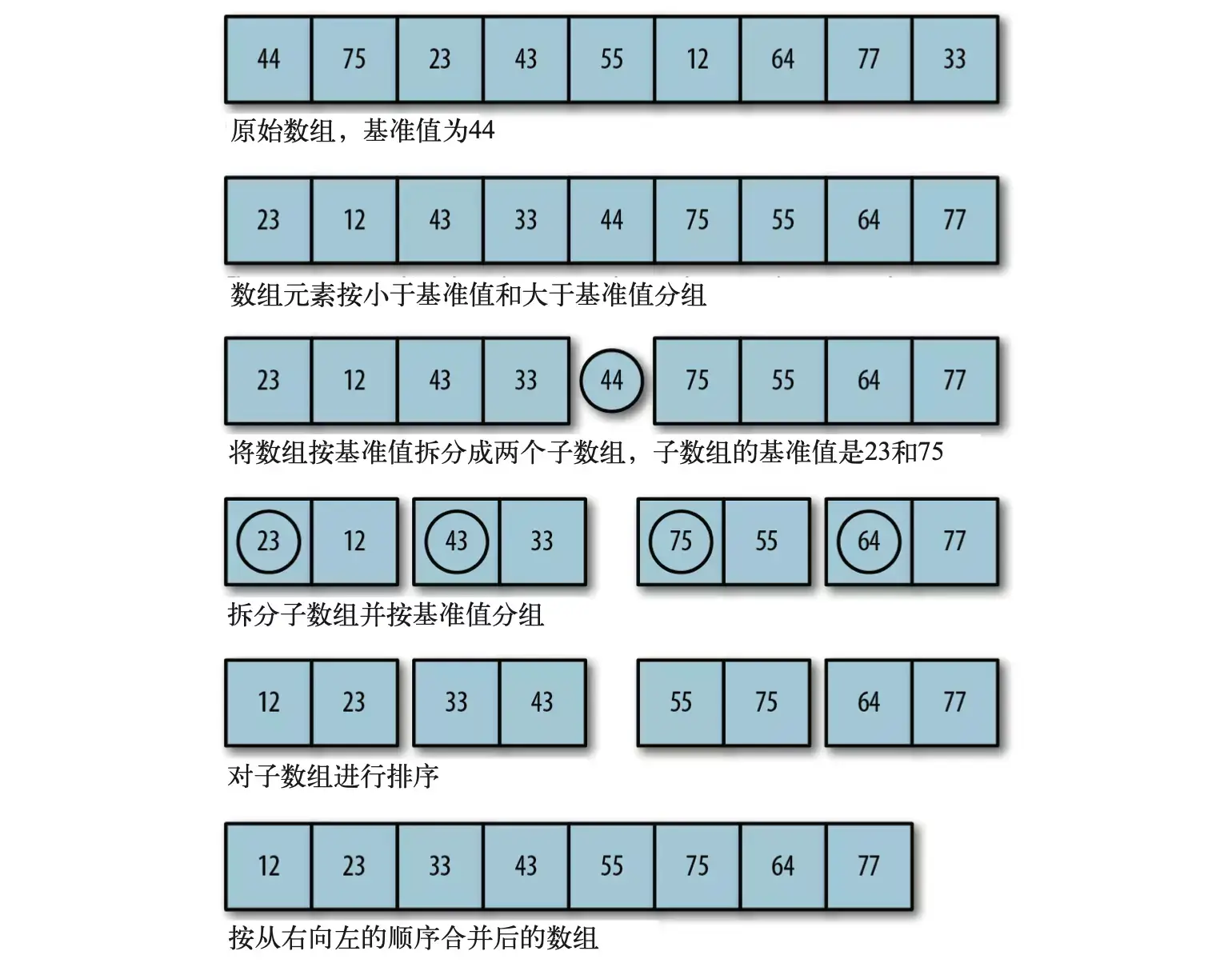
算法过程：

1. 找到一个基准值（pivot），将待排序数组分成两个字数组
2. 将小于基准值的值放到左子数组中，大于基准值的值放到右子数组中。依次类推，最终将各个子数组合并

// 快速排序
const quickSort = (arr) => {
  if(!arr.length) return [];

  let leftArr = [], rightArr = [];
  let pivot = arr[0]

  for (let i = 1; i < arr.length; i++) {
    if(arr[i] <= pivot) {
      leftArr.push(arr[i])
    }else {
      rightArr.push(arr[i])
    }
  }
  return quickSort(leftArr).concat(pivot, quickSort(rightArr))
}

该快速排序中在递归中使用了额外的空间，有没有在原地进行操作的方式。

下面有两种方式进行原地操作：

• 双边循环法
• 单边循环法

双边循环法

双边循环法是在对撞指针的基础上，根据基准点（一般第一个元素），将小于基准点的元素移动到其左侧，大于基准点的元素移动到其右侧。

const quickSortMain = (arr) => {
  let start = 0;
  let len = arr.length;
  let end = len - 1;

  quickSort(arr, start, end);
}

const quickSort = (arr, start, end) => {
  if(start >= end) return;
  // 计算基准值
  let pivot = partition(arr, start, end);

  quickSort(arr, start, pivot - 1);
  quickSort(arr, pivot + 1, end);
}

如下图 计算下一轮递归的基准值

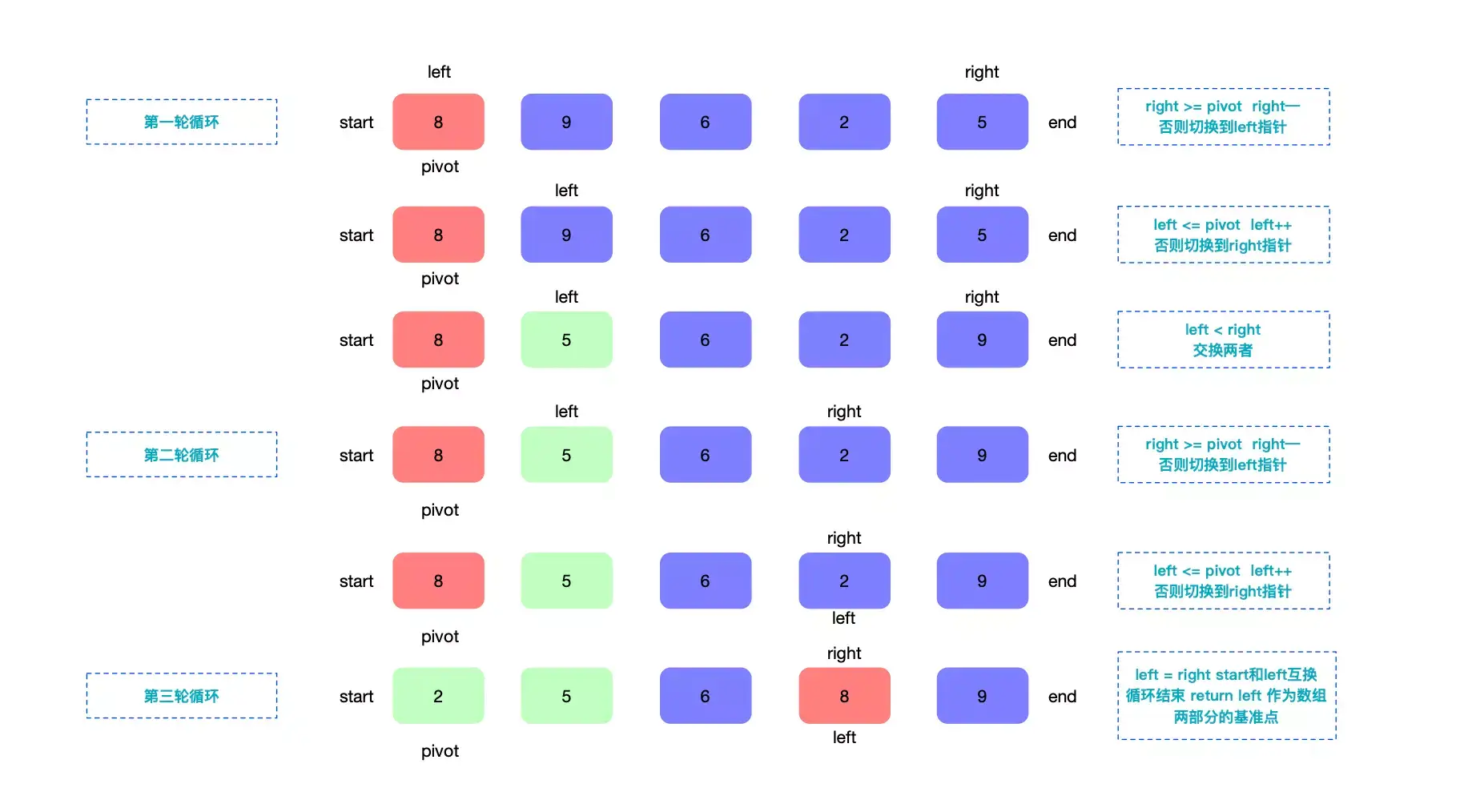
首先从right 右指针开始，对比基准点 pivot ，大于基准点 right 指针向左侧移动，否则移动左指针 left 。

如果left 小于基准点 pivot ，left 左指针向右侧移动，直到left 大于基准点。

此时，left 小于 right，则交换两者的值。进行下一轮循环，直到 left 和 right 相等。

最后，交换基准值和left对应的值，这样基准值左侧就是小于其值的，右侧是大于其值的。最后返回left 作为下一轮递归的基准点。

const partition = (arr, start, end) => {
  let left = start;
  let right = end;
  let pivot = arr[start];

  while(left != right) {

    while(left < right && arr[right] > pivot) {
      right--;
    }

    while(left < right && arr[left] <= pivot) {
      left++;
    }

    if(left < right) {
      let tmp = arr[left];
      arr[left] = arr[right];
      arr[right] = tmp
    }
  }

  arr[start] = arr[left];
  arr[left] = pivot;

  return left;
}

单边循环法

单边循环法是使用一个单指针来遍历，同时pivot基准元素也是取的第一位，增加了 mark 指针，来标记基准元素左右的边界。如下图，计算第一次获取边界值的循环

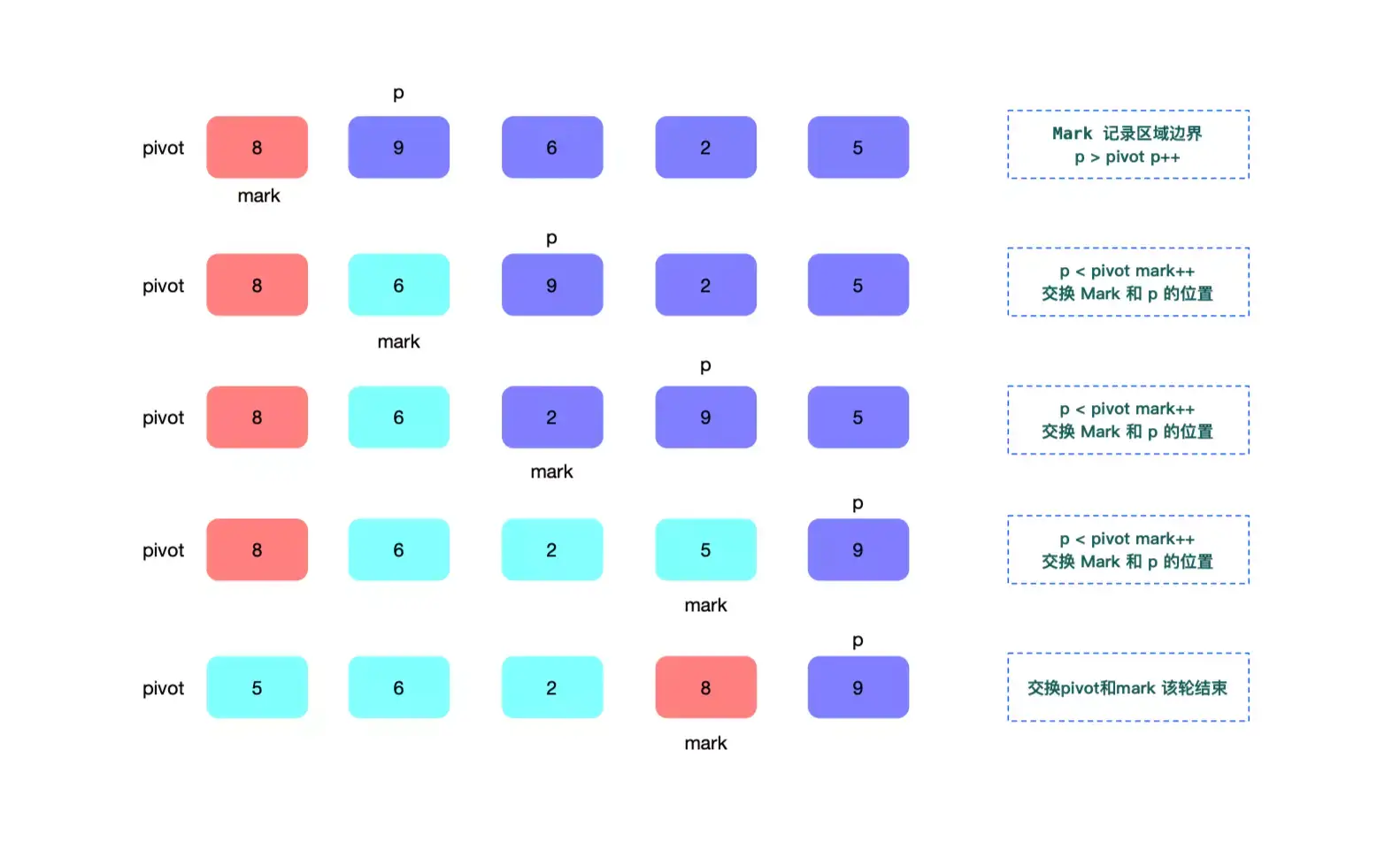
首先记录pivot和mark指针为首位，循环指针p为pivot的下一位，判断 p 和 pivot的大小。

如果 p 大于 pivot，p 继续移动；p 小于 pivot，mark移动一位，之后交换p和mark的值，这样mark边界区分了基准值左右两侧的值。

以此类推，直到p移动结束，交换pivot和mark的值，最终得到了下一轮循环的基准值。

// 这里实现单边循环 其他递归方式以及条件跟上述一致
const partition_single = (arr, start, end) => {

  let pivot = arr[start];
  let mark = start;

  for (let p = start + 1; p <= end; p++) {
    if(arr[p] < pivot) {
      mark++;
      let tmp = arr[p];
      arr[p] = arr[mark];
      arr[mark] = tmp;
    }
  }
  arr[start] = arr[mark];
  arr[mark] = pivot；

  return mark
}

归并排序

归并排序是利用了分治的思想，将原问题拆分成子问题，然后递归的解决子问题，合并子问题的解。

举个例子

给定原问题[4,2,6,3,8,5,9]，将其对半拆分成多个子问题，直到不能拆分位置，然后从子问题出发，排序子问题。

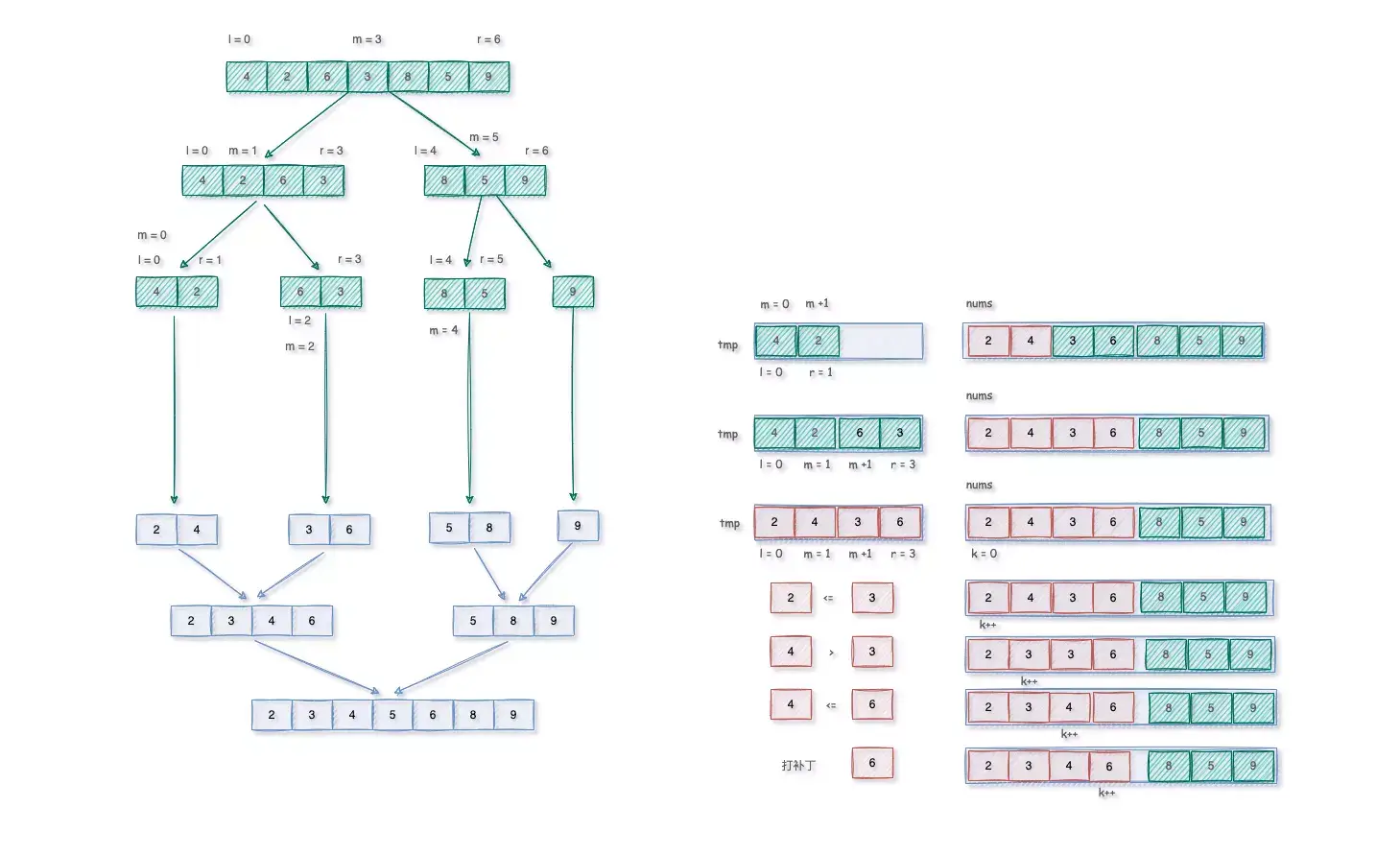
因为使用递归思想，那么必须满足三个条件：

1. 递归结束条件 - 对半拆分数组直到剩下单个元素
2. 拆分原问题 - 对半拆分原问题
3. 合并子问题 - 对已排序的子数组进行合并排序

代码实现：

// 入口函数
const sortArray = nums => {
  let len = nums.length;
  let left = 0, right = len - 1, temp = [];
  sortMerge(left, right, nums, temp);
  return nums;
}

const sortMerge = (left, right, nums, temp) => {

  // 递归结束条件
  if(left >= right) return;

  // 拆分原问题
  let mid = (left + right) >> 1;
  sortMerge(left, mid, nums, temp);
  sortMerge(mid+1, right, nums, temp);

  // 排序合并子问题
  mergeSortArray(left, mid, right, nums, temp)
}

// 合并两个已排序的数组
const mergeSortArray = (left, mid, right, nums, temp) => {

  // 首先暂存原子数组
  for(let i = left; r <= right; i++) {
    temp[i] = nums[i]
  }
  // i 代表temp区间 [left, mid]
  let i = left, k = left;

  // j 代表temp区间 [mid+1, right]
  let j = mid + 1;

  while(i <= mid && j <= right) {
    if(temp[i] <= temp[j]) {
      nums[k++] = temp[i++]
    }else {
      nums[k++] = temp[j++]
    }
  }
  // 打补丁 [left, mid]没有遍历结束
  while(i <= mid) {
    nums[k++] = temp[i++]
  }

  // 打补丁 [mid+1, right]没有遍历结束
  while(j <= right) {
    nums[k++] = temp[j++]
  }
}

可以看到，拆分数组的也是用的深度优先遍历，类似于树的后序遍历。

对于时间复杂度，拆分时间 x 合并时间，因为拆分是对半分，时间为O(logn)，而合并时间是合并两个有序数组的时间，均值为O(n)，因此，总体时间复杂度为O(nlogn)。

空间复杂度，因为使用额外的temp，所以为O(n)。