双指针和滑动窗口

常见的双指针模式有 左右指针 和 快慢指针

双指针 - 左右指针

左右指针最典型的应用就是二分查找了，初次之外，滑动窗口是左右指针的进阶版。

左右指针主要是在数组（字符串）的两端进行移动的，这样做的目的旨在节省时间，更高效的进行查找或者处理元素。

上面图是比较简单的左右指针（反转字符串）移动的动态图。接下来看下代码

编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。
不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。

输入：["h","e","l","l","o"]
输出：["o","l","l","e","h"]

题目要求使用O(1)的时间复杂度，和原地修改，则就说明只能循环一次和不能用额外的空间。

const reverseString = (arr) => {
  let left = 0, right = arr.length - 1;
  while(left <= right) {
    let tmp = arr[left]
    arr[left] = arr[right]
    arr[right] = tmp
    left++;
    right--;
  }
}

两数之和也可以使用双指针来解决

输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。

解法可以使用暴力破解或者哈希解决，但是这两种在时间和空间复杂度都有一定的损耗，最优的可以使用左右双指针模式

const numberSum = (arr, target) => {
  let left = 0, right = arr.length - 1;
  while(left <= right) {
    const curSum = arr[left] + arr[right]
    if(curSum == target) {
      return [left+1, right+1]
    }else if(curSum < target) {
      left++
    }else {
      right--
    }
  }
  return []
}

验证回文串

验证回文串是对撞指针比较典型的应用了，也是比较简单的一种，前后指针同时移动，直到两者相遇。

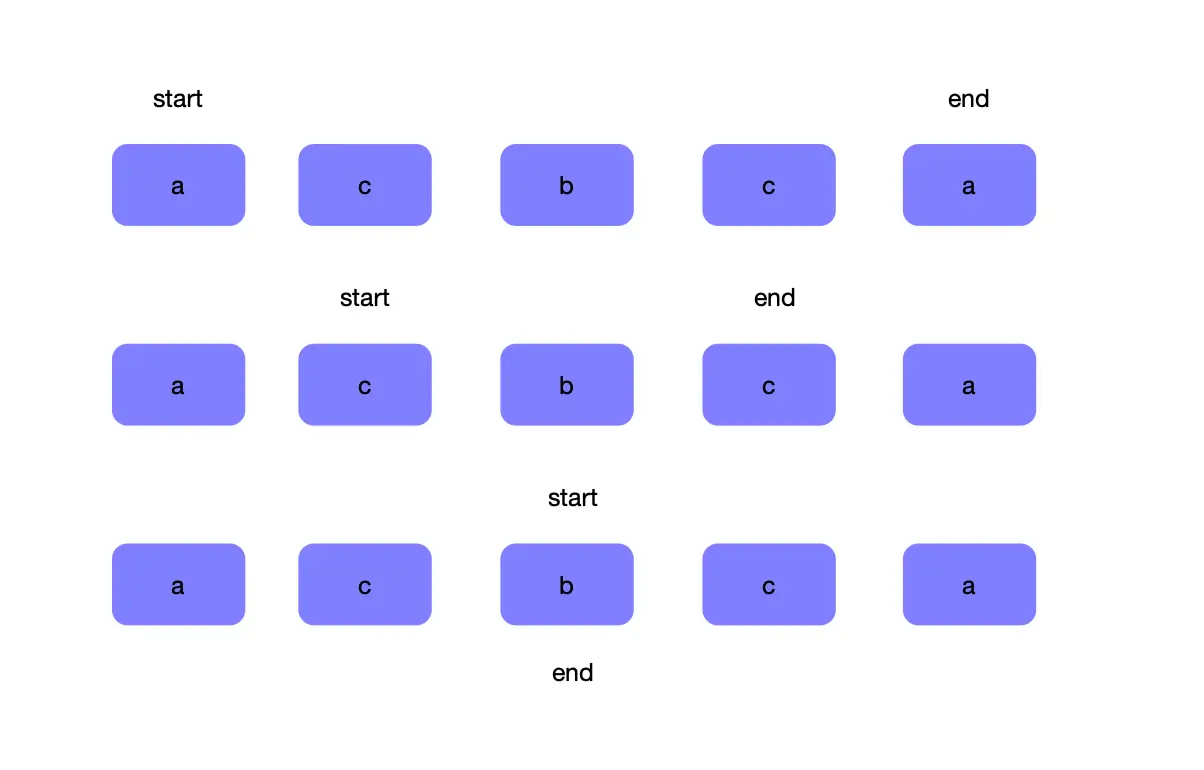
palindrome

算法实现起来也很简单

const isPalindrome = (s) => {
  s = s.replace(/[^0-9A-Za-z]/g, '').toLowerCase();
  let len = s.length;
  let start = 0;
  let end = len - 1;
  while(start < end) {
    if(s[start] != s[end]) return false;
    start++;
    end--;
  }
  return true;
}

反转字符串中的元音字母

输入："hello"
输出："holle"

不难看到，该题也可以用对撞指针解决，但是前后指针在每次循环中不能同时移动，这也是对撞指针的另一种使用场景，如下图，展示反转元音字母的图示

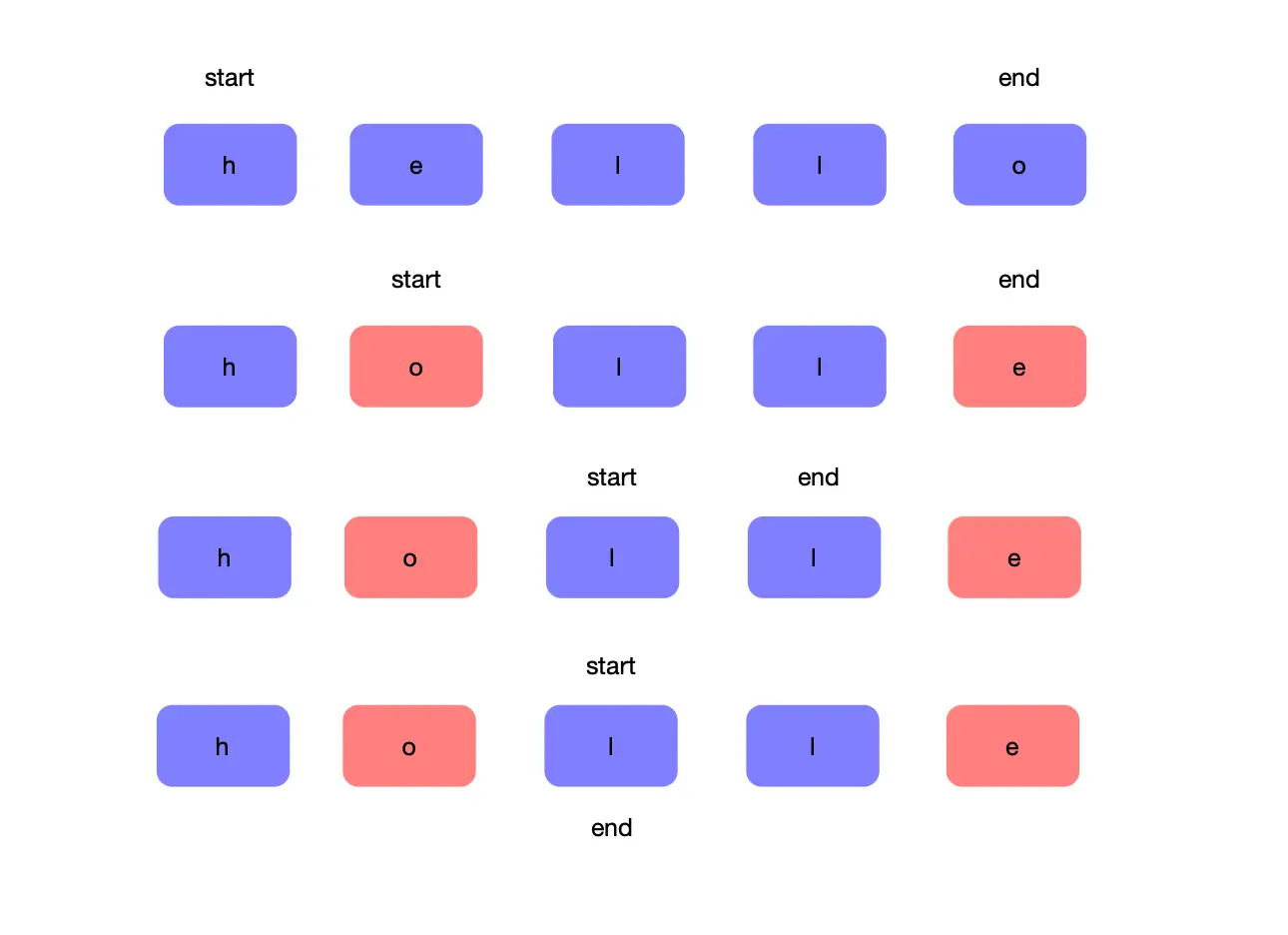
reverseVowels

可以看到start 和 end 分别判断是否是元音字母（a , e, i, o, u）,如果end 不是元音字母，end向前移动，进入下个循环，知道是原因字母；start 也是同理，当 start 和 end 都是元音字母时，交换位置，两者指针分别移动一位，以此类推，直到start 和 end 相遇。

const reverseVowels = function(s) {
  s = s.split('')
  let len = s.length;
  let start = 0;
  let end = len - 1;
  let vowels = ['a', 'e', 'i', 'o', 'u', 'A', 'E', 'I', 'O', 'U'];

  while(start < end) {
    while(start < end && !vowels.includes(s[start])) {
      start++;
    }

    while(start < end && !vowels.includes(s[end])) {
      end--;
    }

    if(vowels.includes(s[start]) && vowels.includes(s[end])) {
      let tmp = s[start];
      s[start] = s[end];
      s[end] = tmp;
    }
    start++;
    end--;
  }
  s.join('')
}

盛最多水的容器

输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，
容器能够容纳水（表示为蓝色部分）的最大值为 49。

如果使用暴力破解法，时间复杂度就很高了，没有必要。这里也可以使用对撞指针的，只遍历一次，在时间复杂度和空间复杂度都是最优的。

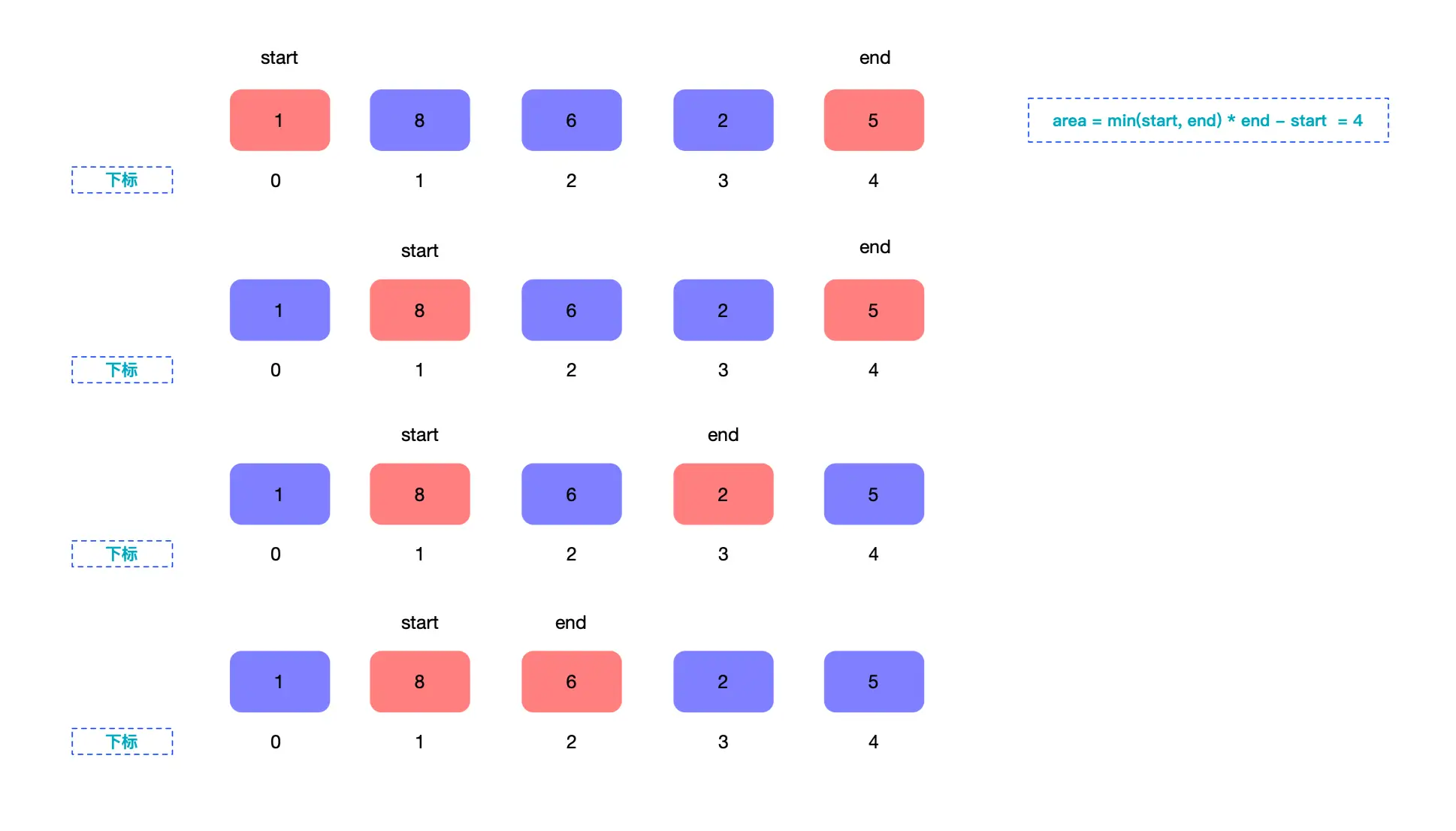
maxArea

上图展示了指针的移动方向，这里如何判断前后指针的移动才能保证整个区域的面积最大？

$$ A(s,e) = Math.min(s,e) * (e - s) $$

当移动短板（数值较小的）的时候 $$Math.min(s,e)$$ 可能变大，其面积可能变大

当移动长板（数值较大的）的时候 $$Math.min(s,e)$$ 可能变小或者不变

因此，当start 和 end 指针指向的值

start < end start++
start > end end--

每次循环记录最大的值，循环结束，最大的就得到了最大的容器

const maxArea = function(height) {
  let len = height.length;
  let start = 0;
  let end = len - 1;
  let maxArea = 0;

  while(start < end) {
    let area = Math.min(height[start], height[end]) * (end - start);

    if(height[start] < height[end]) {
      start++
    }else {
      end--
    }

    maxArea = Math.max(maxArea, area);
  }

  return maxArea;
}

双指针 - 快慢指针

移动零

题目：给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

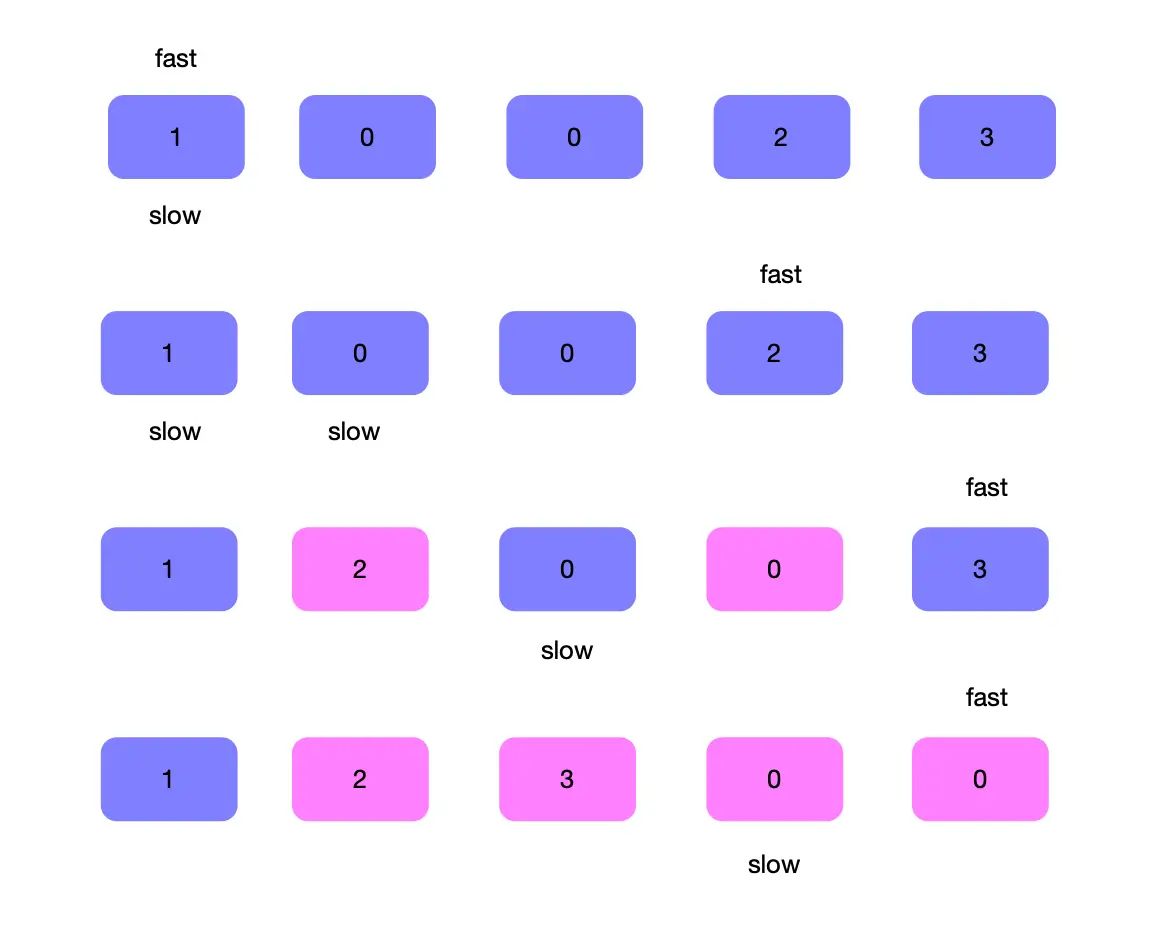
removeZero

上图描述了使用快慢指针移动零的步骤，是简单的双指针应用

const moveZero = (arr) => {
  let f = 0;
  let s = 0;
  let len = arr.length;

  while(f < len) {
    if(arr[f] != 0) {
      let tmp = arr[f];
      arr[f] = arr[s];
      arr[s]= tmp;
      s++
    }
    f++
  }
}

移除元素

移除元素题目也是类似的算法题目。

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2]
解释：函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。
你不需要考虑数组中超出新长度后面的元素。例如，函数返回的新长度为 2 ，
而 nums = [2,2,3,3] 或 nums = [2,2,0,0]，也会被视作正确答案。

解法跟移除零类似，将需要移除的元素移动到数组的末端

const removeElement = (arr, val) => {
  let f = 0;
  let s = 0;
  let len = arr.length;

  while(f < len) {
    if(arr[f] != val) {
      let tmp = arr[f];
      arr[f] = arr[s];
      arr[s] = tmp;
      s++
    }
    f++
  }
  return s
}

删除排序数组中的重复项

给你一个有序数组 nums ，请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，
返回删除后数组的新长度。不要使用额外的数组空间，
你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。

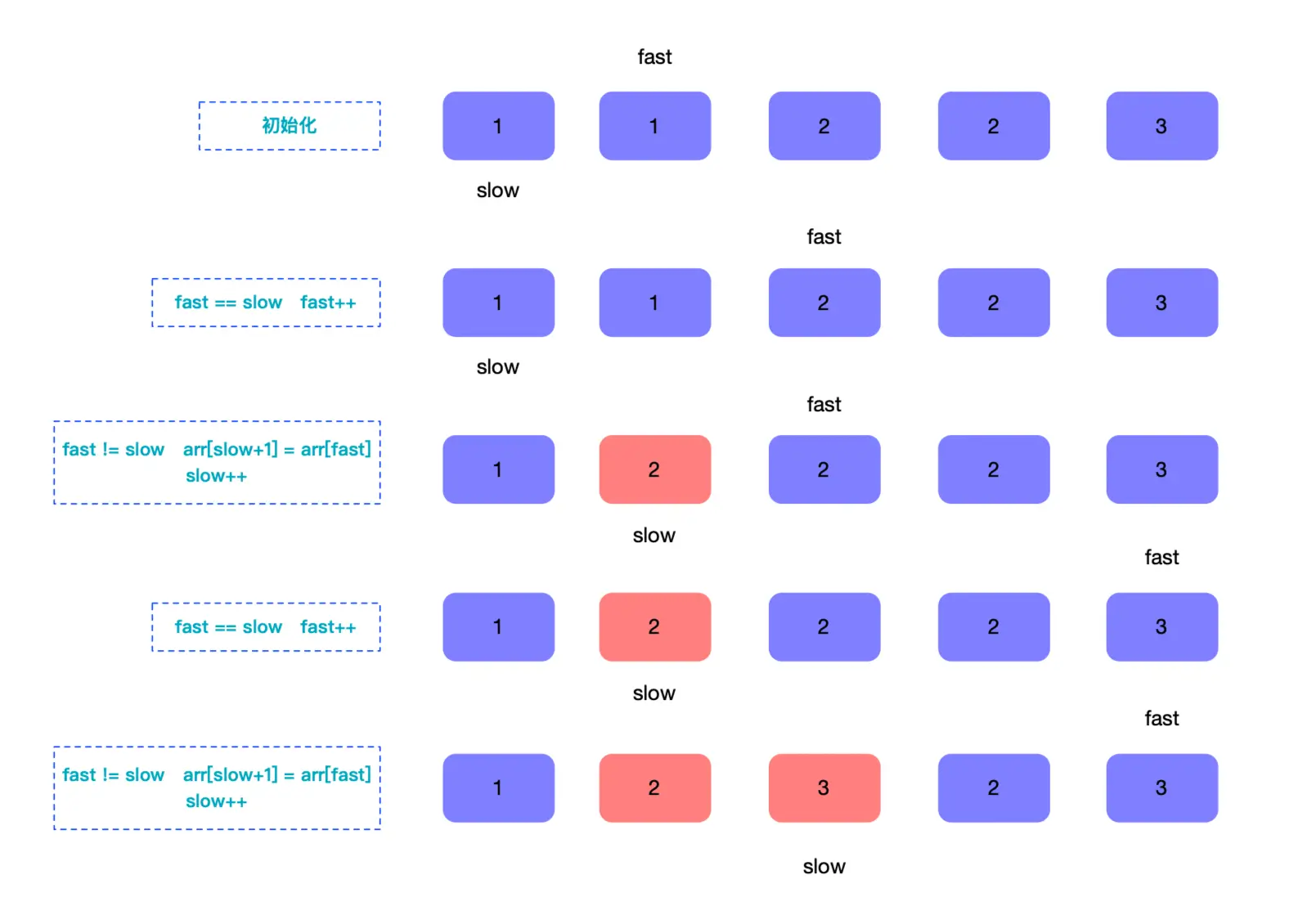
deleteDuplicate

上图使用双指针图示了完整的流程，其中有个技巧就是当 slow 和 fast 指针对应的值不等时， arr[slow + 1] = arr[fast] ，最终slow+1 就是移除重复元素后的数组的长度。

const removeDuplicates = (arr) => {
  let len = arr.length;
  if(len < 2) return len;

  let f = 1;
  let s = 0;
  while(f < length) {
    if(arr[f] != arr[s]) {
      arr[s + 1] = arr[f]
      s++
    }
    f++
  }
  return s + 1
}

删除有序数组中的重复项 II

输入：nums = [1,1,1,2,2,3]
输出：5, nums = [1,1,2,2,3]
解释：函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为 1, 1, 2, 2, 3 。
不需要考虑数组中超出新长度后面的元素。

该题是上者的变形题，只需改变指针的位置即可

const removeDuplicatesII = (arr) => {
  let len = arr.length;
  if(len < 2) return len;
  let s = 2;
  let f = 2;

  while(f < len) {
    if(arr[s - 2] != arr[f]) {
      arr[s] = arr[f]
      s++
    }
    f++
  }
  return s
}

滑动窗口技巧

采用双指针滑动窗口高级技巧可以解决一些很复杂的算法问题，可以用解决数组/字符串的子元素问题，将嵌套的循环问题转换为单循环的问题，类似于最小覆盖字符串等。

这里通过一个简单的例子，熟悉一下什么是滑动窗口模式。

示例：给定一个整数数组，计算长度为k的连续子数组的最大总和?

题意很好理解，找出连续K个子数组，其值是最大值。

先来看下暴力解法

暴力解法就是采用双重循环，将每个连续 K 个数组的和比较，记录其中最大值。

var arr = [100, 200, 150, 300, 250, 350],
  k = 3;

function maxArr(arr) {
  let len = arr.length - k + 1;
  let maxNum = Number.MAX_SAFE_INTEGER;
  let maxCount = 0;

  for (let i = 0; i < len; i++) {
    let curNum = 0;
    for (let j = 0; j < k; j++) {
      curNum += arr[i + j];
    }
    maxCount = Math.max(maxCount, curNum);
  }

  return maxCount;
}

暴力求解的时间复杂度O(len*k)

滑动窗口解法

滑动窗口将多重循环可以简化为单次循环，这里可以将连续的 K 个子数组当做一个窗口，首先获取第一个窗口的和值，下一个窗口的和值为上一个窗口的和值加当前值减掉arr[n-k]，对比前后窗口的值就可以了

function maxSliderArr(arr, k) {
  let len = arr.length;
  if (len < k) {
    return -1;
  }

  let maxNum = 0;
  // 获取第一个窗口的和值
  for (let i = 0; i < k; i++) {
    maxNum += arr[i];
  }

  let curMax = maxNum;

  for (let j = n; j < len; j++) {
    curMax += arr[j] - arr[j - k];
    maxNum = Math.max(maxNum, curMax);
  }

  return maxNum;
}

接下来看下滑动窗口的算法思想:

算法思想

在字符串或者数组中使用双指针（左右指针），left=0, right=0，初始化为 0，将左右指针的闭合区间称之为窗口
开始遍历的时候，先不断增加right，左指针left此时仍为 0，知道当前窗口满足要寻找的所有字符
此时停止增加right，转而增加left，不断的缩小窗口，知道窗口不满足要寻找的字符，每增加一次left，都要更新一轮结果
重复 2，3 步骤

下图借用leetCode的动图

根据这个动图，可以简单的概括滑动窗口的伪代码；

function slideWindowCode(str, tar) {
  let left = 0,
    right = 0;
  let len = str.length;
  let map_window,
    res = str;

  while (right < len) {
    // 进入窗口
    map_window.add(str[right]);
    right++;
    // 整个tar都在窗口中时
    while (tar in map_window) {
      // 获取最小窗口
      res = minLen(res, map_window);
      map_window.remove(str[left]);
      left++;
    }
  }
  return res;
}

下面就LeetCode中有关所有的滑动窗口算法进行分析以及归纳

最小覆盖子串

最小覆盖子串 - LeetCode 是属于hard level，不过使用滑动窗口技巧就不会那么困难了。

算法描述:

# 给你一个字符串 S、一个字符串 T 。请你设计一种算法，可以在 O(n) 的时间复杂度内，从字符串 S 里面找出：包含 T 所有字符的最小子串。

# 示例

输入：S = "ADOBECODEBANC", T = "ABC"
输出："BANC"

# 解析

套用滑动窗口的框架 code，不难发现几个条件点

1. 字符何时进入窗口
   在 right 指针移动时，若当前字符在目标字符中，则该字符进入到窗口，记录窗口中的字符和目标字符中每个字符出现的次数。
2. 如何判断目标字符全部在窗口中
   如果窗口中的每个字符次数和目标窗口的对应字符的次数一致时，则 right 指针停止，计算当前窗口大小以及开始移动 left 指针
3. 如何获取最小窗口
   每移动一次 left 指针，就要更新一次窗口大小，如果当前 left 指针指向的字符在目标字符中，则当前窗口需要移除该字符
4. 何时 right 指针会移动
   在 left 指针移动的过程中，窗口中字符出现的次数和目标字符次数不一致的时候。

下面看下完整的 code:

function slideWindow(str, tar) {
  let left = 0,
    right = 0,
    len = str.length,
    matchs = 0;

  let minLen = Number.MAX_SAFE_INTEGER,
    start = 0;

  // 窗口字符 和 目标字符
  let map_need = {},
    map_window = {};

  // 将目标字符转化为字典模式 { 'a': 1, 'b': 1, 'c': 1 }
  for (let k of tar) {
    if (map_need[k]) {
      map_need[k]++;
    } else {
      map_need[k] = 1;
    }
  }

  while (right < len) {
    let charR = str[right];
    if (map_need[charR]) {
      map_window[charR] = (map_window[charR] || 0) + 1;
      if (map_window[charR] === map_need[charR]) {
        matchs++;
      }
    }
    right++;

    // 当前窗口的字符满足目标字符，则开始移动左指针
    while (matchs === Object.keys(map_need).length) {
      const charL = str[left];
      // 更新窗口大小
      if (right - left < minLen) {
        start = left;
        minLen = right - left;
      }

      // 移除窗口中的字符
      if (map_need[charL]) {
        map_window[charL]--;

        if (map_window[charL] < map_need[charL]) {
          matchs--;
        }
      }
      left++;
    }
  }
  return minLen === Number.MAX_SAFE_INTEGER ? '' : str.substr(start, minLen)
}

找到字符串中所有字母异位词

找到字符串中所有字母异位词 - LeetCode 是属于hard level 算法描述:

# 给定一个字符串  s  和一个非空字符串  p，找到  s  中所有是  p  的字母异位词的子串，返回这些子串的起始索引。

# 字符串只包含小写英文字母，并且字符串  s  和 p  的长度都不超过 20100。

# 示例

输入：s: "cbaebabacd" p: "abc"
输出："[0, 6]"

# 解析

这个跟最小覆盖子串比较类似，其是找到符合最短的满足目标字符的字符长度。
而这个找到字符串中所有字母异位词是寻找完全符合目标字符长度

下面看下完整的 code:

var findAnagrams = function(s, p) {
  let left = 0,
    right = 0;
  (len = s.length), (matchs = 0);
  let mp_need = {};
  let mp_window = {};
  let res = [];

  for (const k of p) {
    if (mp_need[k]) {
      mp_need[k]++;
    } else {
      mp_need[k] = 1;
    }
  }

  while (right < len) {
    let charR = s[right];

    if (mp_need[charR]) {
      mp_window[charR] = (mp_window[charR] || 0) + 1;
      if (mp_need[charR] === mp_window[charR]) {
        matchs++;
      }
    }
    right++;

    while (matchs === Object.keys(mp_need).length) {
      let charL = s[left];
      if (right - left === Object.keys(mp_need).length) {
        res.push(left);
      }
      if (mp_need[charL]) {
        mp_window[charL]--;

        if (mp_window[charL] < mp_need[charL]) {
          matchs--;
        }
      }
      left++;
    }
  }
  return res;
};

无重复字符的最长子串

无重复字符的最长子串 - LeetCode 是属于middle level 算法描述:

# 给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。

# 字符串只包含小写英文字母，并且字符串  s  和 p  的长度都不超过 20100。

# 示例

输入：s: "abcabcbb"
输出：3
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

# 解析

下面看下完整的 code:

/**
 * @param {string} s
 * @return {number}
 */
var lengthOfLongestSubstring = function(s) {
  let left = 0,
    right = 0,
    res = 0,
    len = s.length;
  let map_window = {};

  while (right < len) {
    let charR = s[right];
    map_window[charR] ? map_window[charR]++ : (map_window[charR] = 1);
    right++;

    while (map_window[charR] > 1) {
      let charL = s[left];
      map_window[charL]--;
      left++;
    }

    res = Math.max(res, right - left);
  }
  return res;
};

最大连续1的个数 III

最大连续1的个数 III - LeetCode 是属于middle level 算法描述:

# 给定一个由若干 0 和 1 组成的数组 A，我们最多可以将 K 个值从 0 变成 1 。

# 返回仅包含 1 的最长（连续）子数组的长度。

# 示例

输入：A = [1,1,1,0,0,0,1,1,1,1,0], K = 2
输出：6
解释: [1,1,1,0,0,1,1,1,1,1,1]，粗体数字从 0 翻转到 1，最长的子数组长度为 6。

# 解析

这个算法解法跟**无重复字符的最长子串**类似，窗口每滑动一次，都要更新一遍窗口的大小（窗口没有收缩），在窗口每缩小之后，也要更新一遍窗口的大小

完整解题算法

var longestOnes = function(A, K) {
  let left = 0, right = 0, sum = 0, len = A.length;
  let res = 0;

  while(right < len) {
    let charR = A[right];
    (charR === 0 ) && sum++;
    right++;

    while(sum > K) {
      let chatL = A[left];
      (charL === 0) && sum--;
      left++
    }
    res = Math.max(res, right - left)
  }
  return res;
}

滑动窗口的最大值

滑动窗口的最大值 - LeetCode 是属于easy level 算法描述:

# 给定一个数组 nums 和滑动窗口的大小 k，请找出所有滑动窗口里的最大值。

# 示例

输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:

滑动窗口的位置 最大值

---

[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7

# 解析

该算法主要解决的是某一个窗口中最大值，用到了单调队列特殊的数据结构

掌握了单调队列之后，就可以解决这道算法了，下面解题的大概框架

var maxSlidingWindow = function(nums, k) {
  let res = [];
  // 初始化单调队列滑动窗口
  let queue_window = new MonotonicQueue();

  for (let i = 0; i < nums.length; i++) {
    // 先将窗口中 k - 1 个元素入队
    if (i < k - 1) {
      queue_window.push(nums[i]);
    } else {
      // 窗口滑动
      queue_window.push(nums[i]);
      // 获取当前窗口中的最大值
      res.push(queue_window.max());
      // 窗口首位元素出队
      queue_window.pop(nums[i - k + 1]);
    }
  }
};

接下来看下单调队列的实现

class MonotonicQueue {
  constructor() {
    this.queue = [];
  }

  empty() {
    return !this.queue.length;
  }

  size() {
    return this.queue.length || 0;
  }

  // 返回队尾的元素
  back() {
    return this.size() && this.queue[this.size() - 1];
  }
  // 删除队尾元素
  popBack() {
    this.queue.pop();
  }
  // 队尾新增元素
  pushBack(n) {
    this.queue.push(n);
  }

  // 元素入队
  push(n) {
    while (!this.empty() && this.back() < n) {
      this.popBack();
    }
    this.pushBack(n);
  }
  // 返回队首的元素
  front() {
    return this.queue[0];
  }
  // 删除队首元素
  popFront() {
    this.queue.shift();
  }
  // 队首新增元素
  pushFront(n) {
    this.queue.unshift(n);
  }

  // 返回最大元素
  max() {
    return this.front();
  }
  // 删除元素
  pop(n) {
    if (!this.empty() && this.front() === n) {
      this.popFront();
    }
  }
}